题目内容
13.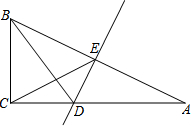 如图,在Rt△ABC中,∠C=Rt∠,AB的垂直平分线交AC于点D,交AB于点E,BD平分∠ABC.
如图,在Rt△ABC中,∠C=Rt∠,AB的垂直平分线交AC于点D,交AB于点E,BD平分∠ABC.(1)求∠A,∠ABC的度数;
(2)连结CE,求证:△BCE是等边三角形.
分析 (1)根据线段垂直平分线上的点到线段两端点的距离相等可得AD=BD,根据等边对等角可得∠DBA=∠A,然后利用直角三角形两锐角互余列式求出∠CBD=∠DBA=∠A=30°;
(2)根据直角三角形斜边的中线等于斜边的一半可得BE=CE,根据等边三角形的判定方法即可得出△BCE是等边三角形.
解答 解:(1)∵DE垂直平分AB,
∴AD=BD,AE=BE,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵∠ABD+∠CBD+∠A=90°
∴∠CBD=∠DBA=∠A=30°;
∴∠ABC=60°;
(2)∵CE是斜边AB的中线,
∴BE=CE,
∵∠ABC=60°,
∴△BCE是等边三角形.
点评 本题考查了等边三角形的判定和性质以及线段垂直平分线上的点到线段两端点的距离相等的性质,角平分线上的点到角的两边的距离相等的性质,等边对等角的性质,以及三角形的内角和定理,熟记各性质是解题的关键.

练习册系列答案
相关题目
4.若(am+1bn+2)•(-a2n-1b2m)=-a3b5,则m+n的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | -3 |
5.若a-3是一个数的算术平方根,则( )
| A. | a≥0 | B. | a≥3 | C. | a>0 | D. | a>3 |
2.下列计算正确的是( )
| A. | 2a-a=2 | B. | x3+x3=x6 | C. | a2•b2=(ab)4 | D. | 2t2+t2=3t2 |
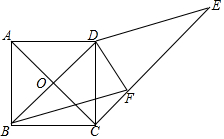 如图,正方形ABCD的边长为1,对角线交于点O,作∠DBF=30°,CE∥BD,DE∥BF,CE与BF交于点F,连接DF,∠DFC=105°.
如图,正方形ABCD的边长为1,对角线交于点O,作∠DBF=30°,CE∥BD,DE∥BF,CE与BF交于点F,连接DF,∠DFC=105°. 如图,已知∠ADE=70°,DF平分∠ADE,∠2=35°,求证:DF∥BE.
如图,已知∠ADE=70°,DF平分∠ADE,∠2=35°,求证:DF∥BE.