题目内容
11.把下列各数分别填在表示它所在的集合里:-5,-$\frac{3}{4}$,0,-(-3.14),-2.4,$\frac{22}{7}$,2003,-1.99,-(-6),-|-12|(1)正分数集合:{-(-3.14),$\frac{22}{7}$ …};
(2)非负数集合:{0,-(-3.14),$\frac{22}{7}$,2003,-(-6) …};
(3)整数集合:{-5,0,2003,-(-6),-|-12| …};
(4)非负整数集合:{0,2003,-(-6) …};
(5)有理数集合:{-5,-$\frac{3}{4}$,0,-(-3.14),-2.4,$\frac{22}{7}$,2003,-1.99,-(-6),-|-12| …}.
分析 (1)根据大于零的分数是正分数,可得正分数集合;
(2)根据大于等于零的数是非负数,可得非负数集合;
(3)整数(像-2,-1,0,1,2这样的数;
(4)根据大于等于零的整数是非负整数,可得非负整数集合;
(5)根据有理数的定义可得有理数集合.
解答 解:(1)正分数集合:{-(-3.14),$\frac{22}{7}$ …};
(2)非负数集合:{ 0,-(-3.14),$\frac{22}{7}$,2003,-(-6)…};
(3)整数集合:{-5,0,2003,-(-6),-|-12|…};
(4)非负整数集合:{ 0,2003,-(-6)…};
(5)有理数集合:{-5,-$\frac{3}{4}$,0,-(-3.14),-2.4,$\frac{22}{7}$,2003,-1.99,-(-6),-|-12|…}.
故答案为:(1){-(-3.14),$\frac{22}{7}$ …};(2){ 0,-(-3.14),$\frac{22}{7}$,2003,-(-6)…};(3){-5,0,2003,-(-6),-|-12|…};(4){ 0,2003,-(-6)…};(5){-5,-$\frac{3}{4}$,0,-(-3.14),-2.4,$\frac{22}{7}$,2003,-1.99,-(-6),-|-12|…}.
点评 本题主要考查的是有理数的定义以及其正分数、非负数、整数和非负整数的定义,比较简单.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.在平面直角坐标系中,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点M为顶点,连接OM,若y与x的部分对应值如表所示:
(1)求抛物线的解析式;
(2)抛物线与y轴交于点C,点Q是直线BC下方抛物线上一点,点Q的横坐标为xQ.若S△BCQ≥$\frac{1}{2}$S△BOC,求xQ的取值范围;
(3)如图2,平移此抛物线使其顶点为坐标原点,P(0,-1)为y轴上一点,E为抛物线上y轴左侧的一个动点,从E点发出的光线沿EP方向经过y轴上反射后与此抛物线交于另一点F.则当E点位置变化时,直线EF是否经过某个定点?如果是,请求出此定点的坐标;若不是,请说明理由.
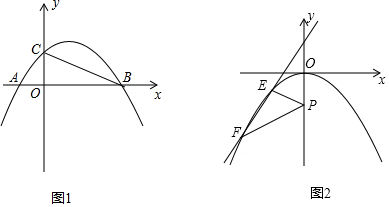
| x | … | -1 | 0 | 3 | … |
| y | … | 0 | 3/2 | 0 | … |
(2)抛物线与y轴交于点C,点Q是直线BC下方抛物线上一点,点Q的横坐标为xQ.若S△BCQ≥$\frac{1}{2}$S△BOC,求xQ的取值范围;
(3)如图2,平移此抛物线使其顶点为坐标原点,P(0,-1)为y轴上一点,E为抛物线上y轴左侧的一个动点,从E点发出的光线沿EP方向经过y轴上反射后与此抛物线交于另一点F.则当E点位置变化时,直线EF是否经过某个定点?如果是,请求出此定点的坐标;若不是,请说明理由.