题目内容
13.如图所示,在等边△OAB中,OB=4,点A在第一象限.(1)点A的坐标为(2,2$\sqrt{3}$);
(2)在坐标平面内存在3个点C,使得以A、O、B、C为顶点的四边形为平行四边形;
(3)在(2)的条件下,若点C为第一象限的点,且点P从点O出发,以每秒1个单位的速度沿x轴的正方向移动,点Q从点B同时出发,以同样的速度沿射线BC的方向移动,试判断△APQ的形状;
(4)当△APQ周长最小时,求出直线PQ的关系式.
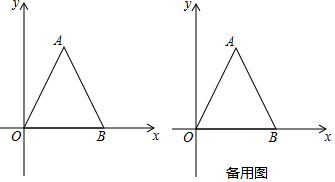
分析 (1)过A作AF⊥OB于点F,由等边三角形的性质可求得OF和AF的长,可求得A点坐标;
(2)有三种情形,根据(1)中结果,直接写出答案即可.
(3)结论:△APQ是等边三角形.只要证明△AOP≌△BAQ,即可推出AP=AQ,∠OAP=∠BAQ,推出∠PAQ=∠OAB=60°.
(4)当AP⊥OB时,△APQ的周长最小,求出P、Q的坐标利用待定系数法即可解决问题.
解答 解:(1)如图1中,作AF⊥OB于F.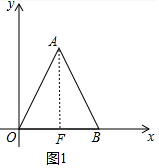
∵△AOB是等边三角形,
∴OA=OB=AB=4,∠AOF=60°,
在Rt△AOF中,∵∠AFO=90°,
∴∠OAF=30°,
∴OF=$\frac{1}{2}$OA=2,AF=OA•tan60°=2$\sqrt{3}$,
∴点A的坐标为(2,2$\sqrt{3}$).
(2)如图2中,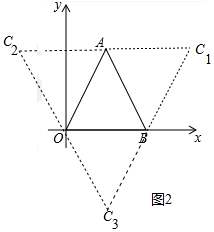
当点C的坐标为(6,2$\sqrt{3}$)或(-2,2$\sqrt{3}$)或(2,-2$\sqrt{3}$)时,以A、O、B、C为顶点的四边形为平行四边形;
故答案为3.
(3)结论:△APQ是等边三角形.理由如下,
如图3中,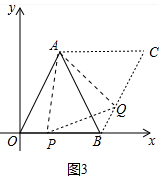
∵△AOB,△ABC都是等边三角形,
∴OB=AB,∠AOP=∠ABQ=∠OAB=60°,
∵OP=BQ,
在△AOP和△ABQ中,
$\left\{\begin{array}{l}{OA=BA}\\{∠AOP=∠ABQ}\\{OP=BQ}\end{array}\right.$,
∴△AOP≌△BAQ,
∴AP=AQ,∠OAP=∠BAQ,
∴∠PAQ=∠OAB=60°,
∴△APQ是等边三角形.
(4)如图3中,∵当AP⊥OB时,△APQ的周长最小,
∴OP=PB=2,BQ=OP=CQ=2,
∴P(2,0),Q(5,$\sqrt{3}$),
设直线PQ的解析式为y=kx+b,则有$\left\{\begin{array}{l}{2k+b=0}\\{5k+b=\sqrt{3}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{\sqrt{3}}{3}}\\{b=-\frac{2\sqrt{3}}{3}}\end{array}\right.$,
∴直线PQ的解析式为y=$\frac{\sqrt{3}}{3}$x-$\frac{2\sqrt{3}}{3}$.
点评 本题考查一次函数综合题、等边三角形的判定和性质、平行四边形的判定和性质、全等三角形的判定和性质等知识,解题的关键是灵活运用所学知识,学会寻找全等三角形解决问题,属于中考压轴题.

 已知:∠α,∠β.请你用直尺和圆规作一个∠BAC,使∠BAC=∠α+∠β.(要求:要保留作图痕迹)
已知:∠α,∠β.请你用直尺和圆规作一个∠BAC,使∠BAC=∠α+∠β.(要求:要保留作图痕迹)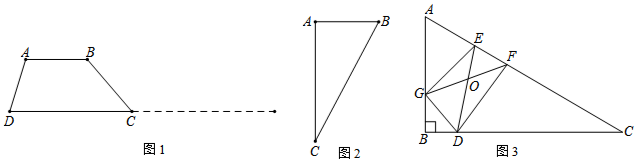
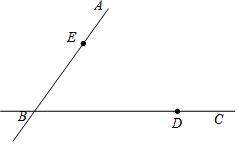 利用尺规作图(不写作法,保留作图痕迹)
利用尺规作图(不写作法,保留作图痕迹) 如图是一个正方体的平面展开图,试问:将其折叠成正方体后,红、黄、绿的对面分别是什么面?
如图是一个正方体的平面展开图,试问:将其折叠成正方体后,红、黄、绿的对面分别是什么面?