题目内容
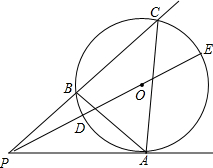 如图,P为⊙O外一点,PA切⊙O于点A.过点P的任一直线交⊙O于B、C两点,连接AB、AC,连接PO并延长交⊙O于D、E两点.
如图,P为⊙O外一点,PA切⊙O于点A.过点P的任一直线交⊙O于B、C两点,连接AB、AC,连接PO并延长交⊙O于D、E两点.(1)求证:∠PAB=∠C;
(2)如果PA2=PD•PE,则当PA=2,PD=1时,求⊙O的半径.
考点:切线的性质,相似三角形的判定与性质
专题:
分析:(1)过A点作直径AF,连接BF,求得∠ABF=90°,即∠F+∠BAF=90°,PA切⊙O于点A.得出∠PAF=90°,即∠PAB+∠BAF=90°,从而求得∠PAB=∠F,根据同弧所对的圆周角相等得出∠F=∠C,进而求得∠PAB=∠C;
(2)根据切割线定理得出PA2=PD•PE,进而求得PE=4,因为DE=PE-PD,即可求得圆的直角,从而求得圆的半径.
(2)根据切割线定理得出PA2=PD•PE,进而求得PE=4,因为DE=PE-PD,即可求得圆的直角,从而求得圆的半径.
解答: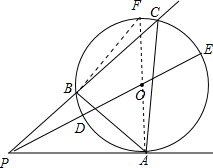 (1)证明:过A点作直径AF,连接BF,
(1)证明:过A点作直径AF,连接BF,
∴∠ABF=90°,
∴∠F+∠BAF=90°,
∵PA切⊙O于点A.
∴∠PAF=90°,
∴∠PAB+∠BAF=90°
∴∠PAB=∠F,
∵∠F=∠C,
∴∠PAB=∠C;
(2)解:∵PA切⊙O于点A,PDE是⊙O的割线,
∴PA2=PD•PE,
∵PA=2,PD=1,
∴PE=4,
∴DE=PE-PD=4-1=3,
∴OD=OE=
,
∴⊙O的半径为
;
 (1)证明:过A点作直径AF,连接BF,
(1)证明:过A点作直径AF,连接BF,∴∠ABF=90°,
∴∠F+∠BAF=90°,
∵PA切⊙O于点A.
∴∠PAF=90°,
∴∠PAB+∠BAF=90°
∴∠PAB=∠F,
∵∠F=∠C,
∴∠PAB=∠C;
(2)解:∵PA切⊙O于点A,PDE是⊙O的割线,
∴PA2=PD•PE,
∵PA=2,PD=1,
∴PE=4,
∴DE=PE-PD=4-1=3,
∴OD=OE=
| 3 |
| 2 |
∴⊙O的半径为
| 3 |
| 2 |
点评:本题考查了圆的切线的性质,圆周角定理,切割线定理等,是中档题,解题时要注意圆周角定理的应用和切割线定理的合理运用.

练习册系列答案
相关题目
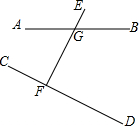 如图,直线AB、CD被EF所截,交点分别为G、F,∠CFG=∠DFG=
如图,直线AB、CD被EF所截,交点分别为G、F,∠CFG=∠DFG=