题目内容
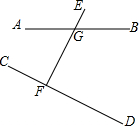 如图,直线AB、CD被EF所截,交点分别为G、F,∠CFG=∠DFG=
如图,直线AB、CD被EF所截,交点分别为G、F,∠CFG=∠DFG=| 3 |
| 4 |
(1)求CD与EF的位置关系?并说明理由;
(2)求∠CFG的同位角、内错角、同旁内角的度数.
考点:垂线,同位角、内错角、同旁内角
专题:
分析:(1)先由∠CFG+∠DFG=180°及∠CFG=∠DFG,可得∠CFG=∠DFG=90°,再根据垂直的定义得到CD与EF互相垂直;
(2)先由∠CFG=∠DFG=
∠AGE,可得∠AGE=120°,再根据同位角、内错角、同旁内角的定义即可求解.
(2)先由∠CFG=∠DFG=
| 3 |
| 4 |
解答:解:(1)CD⊥EF,理由如下:
∵CD是直线,
∴∠CFG+∠DFG=180°,
∵∠CFG=∠DFG,
∴∠CFG=∠DFG=90°,
∴CD⊥EF;
(2)∵∠CFG=∠DFG=
∠AGE=90°,
∴∠AGE=120°,
∴∠CFG的同位角∠AGE=120°,
∠CFG的内错角∠BGF=∠AGE=120°,
∠CFG的同旁内角∠AGF=180°-∠AGE=60°.
∵CD是直线,
∴∠CFG+∠DFG=180°,
∵∠CFG=∠DFG,
∴∠CFG=∠DFG=90°,
∴CD⊥EF;
(2)∵∠CFG=∠DFG=
| 3 |
| 4 |
∴∠AGE=120°,
∴∠CFG的同位角∠AGE=120°,
∠CFG的内错角∠BGF=∠AGE=120°,
∠CFG的同旁内角∠AGF=180°-∠AGE=60°.
点评:本题考查了垂直的定义,邻补角的定义,同位角、内错角、同旁内角的定义,以及对顶角和邻补角的性质的计算,是基础知识,比较简单.

练习册系列答案
相关题目
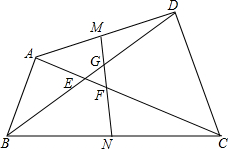 如图,BD=AC,M、N分别为AD、BC的中点,AC、BD交于E,MN与BD、AC分别交于点F、G,求证:EF=EG.
如图,BD=AC,M、N分别为AD、BC的中点,AC、BD交于E,MN与BD、AC分别交于点F、G,求证:EF=EG.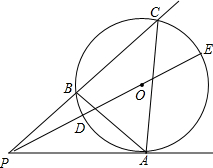 如图,P为⊙O外一点,PA切⊙O于点A.过点P的任一直线交⊙O于B、C两点,连接AB、AC,连接PO并延长交⊙O于D、E两点.
如图,P为⊙O外一点,PA切⊙O于点A.过点P的任一直线交⊙O于B、C两点,连接AB、AC,连接PO并延长交⊙O于D、E两点. 如图,AB∥CD,EF交CD于点H,EG⊥AB,垂足为G.若∠CHE=125°,求∠FEG的度数.
如图,AB∥CD,EF交CD于点H,EG⊥AB,垂足为G.若∠CHE=125°,求∠FEG的度数.