题目内容
已知a、b、c是△ABC的三边,且a+b+c=60cm,a:b:c=3:4:5,求△ABC的面积.
考点:勾股定理的逆定理,三元一次方程组的应用
专题:
分析:先由a+b+c=60cm,a:b:c=3:4:5,求出a、b、c的值,再根据勾股定理的逆定理可求出此三角形为直角三角形,从而可求出面积.
解答:解:∵a+b+c=60cm,a:b:c=3:4:5,
∴a=15cm,b=20cm,c=25cm.
∵152+202=252,
∴△ABC是直角三角形.
∴△ABC的面积为:
×15×20=150.
∴a=15cm,b=20cm,c=25cm.
∵152+202=252,
∴△ABC是直角三角形.
∴△ABC的面积为:
| 1 |
| 2 |
点评:本题考查勾股定理的逆定理,关键根据三边长判断出为直角三角形,然后可求出三角形面积.

练习册系列答案
相关题目
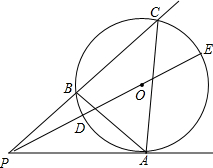 如图,P为⊙O外一点,PA切⊙O于点A.过点P的任一直线交⊙O于B、C两点,连接AB、AC,连接PO并延长交⊙O于D、E两点.
如图,P为⊙O外一点,PA切⊙O于点A.过点P的任一直线交⊙O于B、C两点,连接AB、AC,连接PO并延长交⊙O于D、E两点.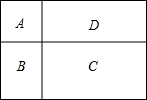 某农科站有一块长方形试验田,面积为1200m2.现要将其分为A、B、C、D四个区,其中A区为正方形.C区的长是30m,宽是20m.求A区的面积是多少平方米?
某农科站有一块长方形试验田,面积为1200m2.现要将其分为A、B、C、D四个区,其中A区为正方形.C区的长是30m,宽是20m.求A区的面积是多少平方米?