题目内容
向阳中学数学兴趣小组对关于x的方程(m+1)xm2+1+(m-2)x-1=0提出了下列问题:
(1)是否存在m的值,使方程为一元二次方程?若存在,求出m的值,并解此方程;
(2)是否存在m的值,使方程为一元一次方程?若存在,求出m的值,并解此方程.
(1)是否存在m的值,使方程为一元二次方程?若存在,求出m的值,并解此方程;
(2)是否存在m的值,使方程为一元一次方程?若存在,求出m的值,并解此方程.
考点:一元二次方程的定义,一元一次方程的定义
专题:
分析:(1)根据一元二次方程的定义可得
,可求得m的值,进一步可求出方程的解;
(2)当m2+1=1或m+1=0时方程为一元一次方程,求出m的值,进一步解方程即可.
|
(2)当m2+1=1或m+1=0时方程为一元一次方程,求出m的值,进一步解方程即可.
解答:解:
(1)根据一元二次方程的定义可得
,解得m=1,此时方程为2x2-x-1=0,解得x1=1,x2=-
;
(2)由题可知m2+1=1或m+1=0时方程为一元一次方程
当m2+1=1时,解得m=0,此时方程为-x-1=0,解得x=-1,
当m+1=0时,解得m=-1,此时方程为-3x-1=0,解得x=-
.
(1)根据一元二次方程的定义可得
|
| 1 |
| 2 |
(2)由题可知m2+1=1或m+1=0时方程为一元一次方程
当m2+1=1时,解得m=0,此时方程为-x-1=0,解得x=-1,
当m+1=0时,解得m=-1,此时方程为-3x-1=0,解得x=-
| 1 |
| 3 |
点评:本题主要考查一元二次和一元一次方程的定义,对(2)中容易漏掉m2+1=1的情况.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
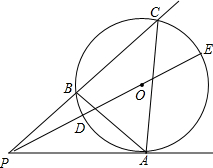 如图,P为⊙O外一点,PA切⊙O于点A.过点P的任一直线交⊙O于B、C两点,连接AB、AC,连接PO并延长交⊙O于D、E两点.
如图,P为⊙O外一点,PA切⊙O于点A.过点P的任一直线交⊙O于B、C两点,连接AB、AC,连接PO并延长交⊙O于D、E两点.