题目内容
在Rt△ABC中,∠C=90°,a=13.5,c=9
,解这个直角三角形.
| 3 |
考点:解直角三角形
专题:
分析:先利用勾股定理求得b边的长,再利用三角函数求得∠A的度数,然后根据直角三角形的两锐角互余求得∠B的度数.
解答:解:在Rt△ABC中,∵∠C=90°,a=13.5,c=9
,
∴b=
=
=
,
∵sinA=
=
=
,
∴∠A=60°,
∴∠B=90°-∠A=90°-60°=30°.
| 3 |
∴b=
| c2-a2 |
(9
|
9
| ||
| 2 |
∵sinA=
| a |
| c |
| 13.5 | ||
9
|
| ||
| 2 |
∴∠A=60°,
∴∠B=90°-∠A=90°-60°=30°.
点评:本题考查了解直角三角形:在直角三角形中,由已知元素求出未知元素的过程就是解直角三角形.正确理解直角三角形中的边角关系是解题的关键.

练习册系列答案
相关题目
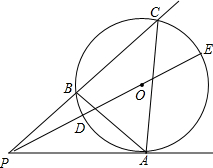 如图,P为⊙O外一点,PA切⊙O于点A.过点P的任一直线交⊙O于B、C两点,连接AB、AC,连接PO并延长交⊙O于D、E两点.
如图,P为⊙O外一点,PA切⊙O于点A.过点P的任一直线交⊙O于B、C两点,连接AB、AC,连接PO并延长交⊙O于D、E两点. 如图,AB∥CD,EF交CD于点H,EG⊥AB,垂足为G.若∠CHE=125°,求∠FEG的度数.
如图,AB∥CD,EF交CD于点H,EG⊥AB,垂足为G.若∠CHE=125°,求∠FEG的度数.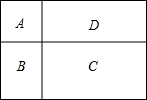 某农科站有一块长方形试验田,面积为1200m2.现要将其分为A、B、C、D四个区,其中A区为正方形.C区的长是30m,宽是20m.求A区的面积是多少平方米?
某农科站有一块长方形试验田,面积为1200m2.现要将其分为A、B、C、D四个区,其中A区为正方形.C区的长是30m,宽是20m.求A区的面积是多少平方米?