题目内容
已知二次函数y=(x-2)2的图象与x轴交于点A,与y轴交于点B,直线PQ过点B与x轴交于点P,与抛物线交于点Q,且OB=OP.求:
(1)直线PQ的解析式;
(2)△ABQ的面积.
(1)直线PQ的解析式;
(2)△ABQ的面积.
考点:抛物线与x轴的交点
专题:
分析:(1)根据题意画出图形,进而利用待定系数法求一次函数解析式进而得出答案;
(2)首先求出Q点坐标,进而利用梯形以及三角形面积公式求出即可.
(2)首先求出Q点坐标,进而利用梯形以及三角形面积公式求出即可.
解答: 解:(1)如图所示:
解:(1)如图所示:
∵二次函数y=(x-2)2的图象与x轴交于点A,与y轴交于点B,
∴y=0时,x=2;x=0时,y=4,
故A(2,0),B(0,4),
∵OB=OP,
∴P(-4,0)或(4,0),
则将B(0,4),P(-4,0)代入y=kx+b得:
,
解得:
.
故直线PQ的解析式为:y=x+4,
当将B(0,4),P(4,0)代入,可得直线解析式为:y=-x+4,
故直线PQ的解析式为:y=-x+4或y=x+4;
(2)当直线PQ的解析式为:y=x+4,
,
解得:
,
,
故抛物线y=(x-2)2与直线y=x+4的交点Q坐标为:(5,9),
故△ABQ的面积为:
(4+9)×5-
×4×2-
×3×9=15.
 解:(1)如图所示:
解:(1)如图所示:∵二次函数y=(x-2)2的图象与x轴交于点A,与y轴交于点B,
∴y=0时,x=2;x=0时,y=4,
故A(2,0),B(0,4),
∵OB=OP,
∴P(-4,0)或(4,0),
则将B(0,4),P(-4,0)代入y=kx+b得:
|
解得:
|
故直线PQ的解析式为:y=x+4,
当将B(0,4),P(4,0)代入,可得直线解析式为:y=-x+4,
故直线PQ的解析式为:y=-x+4或y=x+4;
(2)当直线PQ的解析式为:y=x+4,
|
解得:
|
|
故抛物线y=(x-2)2与直线y=x+4的交点Q坐标为:(5,9),
故△ABQ的面积为:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题主要考查了抛物线与x轴交点问题以及待定系数法求一次函数解析式,得出Q点坐标是解题关键.

练习册系列答案
相关题目
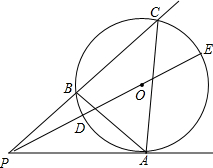 如图,P为⊙O外一点,PA切⊙O于点A.过点P的任一直线交⊙O于B、C两点,连接AB、AC,连接PO并延长交⊙O于D、E两点.
如图,P为⊙O外一点,PA切⊙O于点A.过点P的任一直线交⊙O于B、C两点,连接AB、AC,连接PO并延长交⊙O于D、E两点.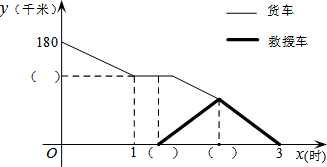 甲地与乙地相距180千米.一辆装载物资的货车从甲地开往乙地,在行驶途中突发故障,司机马上通报乙地并立即维修.12分钟后,乙地派出救援车前往接应.经过抢修,货车在救援车出发8分钟后修复并继续按原速行驶.当两车在途中相遇时,为了确保物资能准时运到,将物资全部转移到救援车上,救援车沿原路按原速返回,并按货车的预计时间到达乙地.下图是货车、救援车距乙地的距离y(千米)与货车出发时间x(时)之间的函数图象(装卸货物时间忽略不计).
甲地与乙地相距180千米.一辆装载物资的货车从甲地开往乙地,在行驶途中突发故障,司机马上通报乙地并立即维修.12分钟后,乙地派出救援车前往接应.经过抢修,货车在救援车出发8分钟后修复并继续按原速行驶.当两车在途中相遇时,为了确保物资能准时运到,将物资全部转移到救援车上,救援车沿原路按原速返回,并按货车的预计时间到达乙地.下图是货车、救援车距乙地的距离y(千米)与货车出发时间x(时)之间的函数图象(装卸货物时间忽略不计). 如图,AB∥CD,EF交CD于点H,EG⊥AB,垂足为G.若∠CHE=125°,求∠FEG的度数.
如图,AB∥CD,EF交CD于点H,EG⊥AB,垂足为G.若∠CHE=125°,求∠FEG的度数.