题目内容
6.已知:点M、N分别是线段AB、BP的中点,点B在线段AP的延长线上,AM-PN=3.5,点C为直线AB上一点,CA-CP=5,求CP的长度.分析 先根据点M、N分别是线段AB、BP的中点,AM-PN=3.5,求得AP的长,再根据点C的位置分类讨论,即可得到CP的长.
解答 解:如图所示,∵点M、N分别是线段AB、BP的中点,
∴AM=$\frac{1}{2}$AB,PN=$\frac{1}{2}$BP,
又∵AM-PN=3.5,
∴$\frac{1}{2}$AB-$\frac{1}{2}$BP=3.5,即AB-BP=7,
∴AP=7,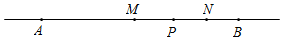
当C在A的左侧时,CA<CP(不合题意),
当C在P的右侧时,CA-CP=AP=7(不合题意),
当C在A、P之间时,根据CA-CP=5,CA+CP=7,可得CP=1,
综上所述,CP的长度为1.
点评 本题主要考查了两点间的距离,连接两点间的线段的长度叫两点间的距离.解决问题的关键是画出图形,进行分类讨论.

练习册系列答案
相关题目
1.不等式x<$\frac{2x+2}{3}$的正整数解的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
11.若|x+y-5|+(x-y+3)2=0,则x2-y2的结果是( )
| A. | 2 | B. | 8 | C. | 15 | D. | -15 |
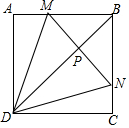 如图,在正方形ABCD中,点M、N分别在AB、BC上,△DMN是等边三角形,连接BD交MN于P,给出下列结论:①AM=CN;②∠CDN=15°;③BD垂直平分MN;④AM+CN=MN,其中结论正确的共有( )
如图,在正方形ABCD中,点M、N分别在AB、BC上,△DMN是等边三角形,连接BD交MN于P,给出下列结论:①AM=CN;②∠CDN=15°;③BD垂直平分MN;④AM+CN=MN,其中结论正确的共有( )