题目内容
1．不等式x＜$\frac{2x+2}{3}$的正整数解的个数是（ ）| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
分析 求出x的范围，从而可求出x的正整数解．
解答 解：3x＜2x+2
x＜2
∵x是正整数
∴x=1
故选（B）
点评 本题考查一元一次不等式，解题的关键是熟练运用一元一次不等式的解法，本题属于基础题型．
练习册系列答案
相关题目
11．已知线段AB=10cm，在直线AB上取一点C，使AC=16cm，则线段AB的中点与AC的中点的距离为（ ）
| A． | 13cm | B． | 6cm | C． | 6cm或26cm | D． | 3cm或13cm |
如图，BD是△ABC的角平分线，它的垂直平分线分别交AB、BC于点E、F、G，连接ED、DG．
13．若$\left\{\begin{array}{l}{x=-3}\\{y=2}\end{array}\right.$是$\left\{\begin{array}{l}{αx+θy=1}\\{θx-βy=-2}\end{array}\right.$的解，则α、β之间的关系是（ ）
| A． | β-9α=1 | B． | 9α+4β=1 | C． | 3α+2β=1 | D． | 4β-9α+1=0 |
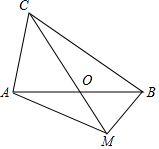如图，在△ABC中，AB=BC=8，AO=BO，点M是射线CO上的一个动点，∠AOC=60°，则当△ABM为直角三角形时，AM的长为4$\sqrt{3}$或4$\sqrt{7}$或4．