题目内容
4.化简求值:已知x,y满足:x2+y2-4x+6y+13=0 求代数式[4(xy-1)2-(xy+2)(2-xy)]÷(-$\frac{1}{4}$xy)的值.分析 利用配方法把原式化为平方和的形式,根据非负数的性质求出x、y,把原式化简,代入计算即可.
解答 解:∵x2+y2-4x+6y+13=0,
∴(x-2)2+(y+3)2=0,
∴x-2=0,y+3=0,
解得,x=2,y=-3,
则[4(xy-1)2-(xy+2)(2-xy)]÷(-$\frac{1}{4}$xy)
=(4x2y2-8xy+4-4+x2y2)÷(-$\frac{1}{4}$xy)
=(5x2y2-8xy)÷(-$\frac{1}{4}$xy)
=-20xy+32
=-20×2×(-3)+32
=152.
点评 本题考查的是配方法的应用、非负数的性质、整式的混合运算,掌握配方法的一般步骤、非负数的性质、整式的混合运算法则是解题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
14.一个整数加上-15,和大于0,这个整数可能是( )
| A. | 16.5 | B. | 16 | C. | 15 | D. | 14 |
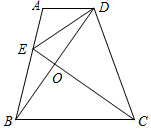 已知:如图,AD∥BC,DB平分∠ADC,CE平分∠BCD,交AB于点E,BD于点O.
已知:如图,AD∥BC,DB平分∠ADC,CE平分∠BCD,交AB于点E,BD于点O.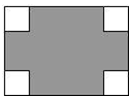 如图,在长为10cm,宽为8cm的矩形的四个角上截去四个全等的小正方形,使得留下的图形(图中阴影部分)面积是原矩形面积的80%,则所截去小正方形的边长是2cm.
如图,在长为10cm,宽为8cm的矩形的四个角上截去四个全等的小正方形,使得留下的图形(图中阴影部分)面积是原矩形面积的80%,则所截去小正方形的边长是2cm.