题目内容
15．
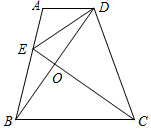已知：如图，AD∥BC，DB平分∠ADC，CE平分∠BCD，交AB于点E，BD于点O．求证：点O到EB与ED的距离相等．
分析 根据平行线的性质和角平分线的定义得到∠DOC=90°，根据等腰三角形的三线合一证明即可．
解答 证明：∵AD∥BC，
∴∠ADC+∠BCD=180°，
∵DB平分∠ADC，CE平分∠BCD，
∴∠ODC+∠OCD=90°，
∴∠DOC=90°，又CE平分∠BCD，
∴CE是BD的垂直平分线，
∴EB=ED，又∠DOC=90°，
∴EC平分∠BED，
∴点O到EB与ED的距离相等．
点评 本题考查的是平行线的性质、角平分线的性质，掌握平行线的判定定理和性质定理是解题的关键．
练习册系列答案
相关题目
5．现定义一种运算“⊙”，对任意有理数m、n，规定：m⊙n=mn（m-n），如1⊙2=1×2（1-2）=-2，则（a+b）⊙（a-b）的值是（ ）
| A． | 2ab2-2b2 | B． | 2a2b-2b3 | C． | 2ab2+2b2 | D． | 2ab-2ab2 |
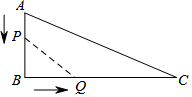如图，在△ABC中，∠B=90°，AB=12cm，BC=24cm，动点P从点A开始沿边AB向B以2cm/s的速度移动，动点Q从点B开始沿BC边向C以4cm/s的速度移动，如果P、Q分别从A、B同时出发，设运动时间为t，△PBQ的面积为S．
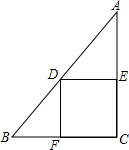如图，在Rt△ABC中，∠C=90°，∠A=30°，AC=8，点D在斜边AB上，分别作DE⊥AC，DF⊥BC，垂足分别为点E，F，得四边形DECF，设DE=x，DF=y．
二次函数y=（x+m）2+n的图象如图，则反比例函数y=$\frac{mn}{x}$的图象经过第一、三象限．
7．下列式子中，能正确表示“x与y的倒数的和”是（ ）
| A． | $\frac{1}{x}$+$\frac{1}{y}$ | B． | $\frac{1}{x}$+y | C． | x+$\frac{1}{y}$ | D． | $\frac{1}{x+y}$ |