题目内容
6．已知扇形的半径为6，圆心角的度数为120°，若将此扇形围成一个圆锥，则围成的圆锥的全面积为（ ）| A． | 9π | B． | 12π | C． | 16π | D． | 18π |
分析 设这个圆的底面半径为r，利用圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长得到2πr=4π，解得r=2，然后计算底面积和侧面积即可．
解答 解：这个扇形的弧长=$\frac{120π×6}{180}$=4π；
设这个圆的底面半径为r，
根据题意得2πr=4π，
解得r=2，
所以这个圆锥的全面积=π•22+$\frac{1}{2}$•2π•2•6=16π．
故选C．
点评 本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
小学期末标准试卷系列答案
相关题目
1．方程|$\frac{x-1}{2}$|+|$\frac{1-x}{3}$|=0的解是（ ）
| A． | 1 | B． | 无数个 | C． | 0 | D． | 无解 |
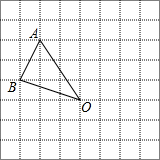在如图所示的方格纸中，每个小方格都是边长为1个单位的正方形，△ABO的三个顶点都在格点上．
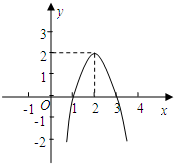二次函数y=ax2+bx+c（a≠0）的图象如图所示，根据图象回答：
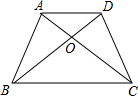如图，四边形ABCD，AD∥BC，对角线AC，BD相交于点O，△AOD和△ABO的面积分别为2cm2和3cm2，求四边形ABCD的面积．
将图中平面展开图折叠成正方体后，相对面上的两个数互为相反数，则x+y+z=-1.5．