题目内容
18.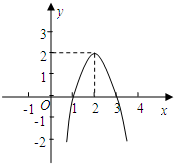 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象回答:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象回答:(1)当y=0时,写出自变量x的值.
(2)当y>0时,写出自变量x的取值范围.
(3)写出y随x的增大而减小的自变量x的取值范围.
(4)若方程ax2+bx+c-k=0有两个不相等的实数根,求k的取值范围(用含a、b、c的代数式表示).
分析 (1)写出抛物线与x轴交点的横坐标即可;
(2)写出抛物线在x轴上方所对应的自变量的范围即可;
(3)根据二次函数的性质求解;
(4)由于方程ax2+bx+c-k=0有两个不相等的实数根,可看作二次函数y=ax2+bx+c与直线y=k有两个交点,则可利用图象法确定k的取值范围.
解答 解:(1)当y=0时,x=1或x=3;
(2)当y>0时,1<x<3;
(3)∵抛物线的开口向下,对称轴为x=2.
∴当x>2时,y随x的增大而减小;
(4)方程ax2+bx+c-k=0变形为ax2+bx+c=k,所以方程ax2+bx+c-k=0有两个不相等的实数根可看作二次函数y=ax2+bx+c与直线y=k有两个交点,如图,
所以k<2,
即k<$\frac{4ac-{b}^{2}}{4a}$.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了二次函数的图象.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.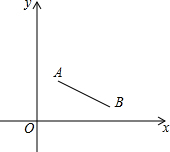 如图,点A、B的坐标分别为(1,2),(3,$\frac{1}{2}$),现将线段AB绕点B顺时针旋转180°得线段A1B,则A1的坐标为( )
如图,点A、B的坐标分别为(1,2),(3,$\frac{1}{2}$),现将线段AB绕点B顺时针旋转180°得线段A1B,则A1的坐标为( )
 如图,点A、B的坐标分别为(1,2),(3,$\frac{1}{2}$),现将线段AB绕点B顺时针旋转180°得线段A1B,则A1的坐标为( )
如图,点A、B的坐标分别为(1,2),(3,$\frac{1}{2}$),现将线段AB绕点B顺时针旋转180°得线段A1B,则A1的坐标为( )| A. | (1,-5) | B. | (5,-2) | C. | (5,-1) | D. | (-1,5) |
6.已知扇形的半径为6,圆心角的度数为120°,若将此扇形围成一个圆锥,则围成的圆锥的全面积为( )
| A. | 9π | B. | 12π | C. | 16π | D. | 18π |
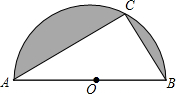 如图,半圆的直径AB,点C在半圆上,已知半径为1,△ABC的周长为$\sqrt{5}$+2,则阴影部分的面积为$\frac{1}{2}π-\frac{1}{4}$.
如图,半圆的直径AB,点C在半圆上,已知半径为1,△ABC的周长为$\sqrt{5}$+2,则阴影部分的面积为$\frac{1}{2}π-\frac{1}{4}$.
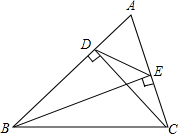 如图,BE,CD是△ABC的两条高.求证:DE•AB=AE•BC.
如图,BE,CD是△ABC的两条高.求证:DE•AB=AE•BC.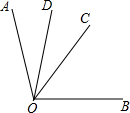 如图,0C是∠A0B的平分线,OD是∠AOC的平分线,且∠BOC+∠COD=75°,求∠BOC和∠COD的度数各是多少度?
如图,0C是∠A0B的平分线,OD是∠AOC的平分线,且∠BOC+∠COD=75°,求∠BOC和∠COD的度数各是多少度?