题目内容
15.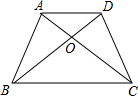 如图,四边形ABCD,AD∥BC,对角线AC,BD相交于点O,△AOD和△ABO的面积分别为2cm2和3cm2,求四边形ABCD的面积.
如图,四边形ABCD,AD∥BC,对角线AC,BD相交于点O,△AOD和△ABO的面积分别为2cm2和3cm2,求四边形ABCD的面积.
分析 等高不同底的三角形的面积比等于底的比得到$\frac{OD}{BO}=\frac{{S}_{△AOD}}{{S}_{△ABO}}$=$\frac{2}{3}$,通过△AOD∽△BOC,根据相似三角形的性质得到$\frac{{S}_{△AOD}}{{S}_{△BOC}}$=($\frac{AD}{BC}$)2=$\frac{4}{9}$,求出S△BOC=$\frac{9}{2}$,即可得到结论.
解答 解:∵△AOD和△ABO的面积分别为2cm2和3cm2,
∴$\frac{OD}{BO}=\frac{{S}_{△AOD}}{{S}_{△ABO}}$=$\frac{2}{3}$,
∵AD∥BC,
∴△AOD∽△BOC,
∴$\frac{{S}_{△AOD}}{{S}_{△BOC}}$=($\frac{AD}{BC}$)2=$\frac{4}{9}$,
∴S△BOC=$\frac{9}{2}$,
∵S△COD=S△AOB=3,
∴四边形ABCD的面积=S△AOD+S△BOC+S△AOB+S△COD=2+$\frac{9}{2}$+3+3=$\frac{25}{2}$.
点评 本题考查了相似三角形的判定和性质,梯形的性质,知道等高不同底的三角形的面积比等于底的比是解题的关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
6.已知扇形的半径为6,圆心角的度数为120°,若将此扇形围成一个圆锥,则围成的圆锥的全面积为( )
| A. | 9π | B. | 12π | C. | 16π | D. | 18π |
 如图所示,在Rt△ABC中,∠C=90°,∠BAC=60°,AB=8.半径为$\sqrt{3}$的⊙M与射线BA相切,切点为N,且AN=3.将Rt△ABC顺时针旋转120°后得到Rt△ADE,点B、C的对应点分别是点D、E.此时Rt△ADE的斜边AD所在的直线与⊙M的位置关系是相切.
如图所示,在Rt△ABC中,∠C=90°,∠BAC=60°,AB=8.半径为$\sqrt{3}$的⊙M与射线BA相切,切点为N,且AN=3.将Rt△ABC顺时针旋转120°后得到Rt△ADE,点B、C的对应点分别是点D、E.此时Rt△ADE的斜边AD所在的直线与⊙M的位置关系是相切.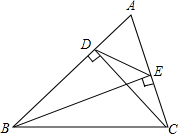 如图,BE,CD是△ABC的两条高.求证:DE•AB=AE•BC.
如图,BE,CD是△ABC的两条高.求证:DE•AB=AE•BC.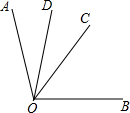 如图,0C是∠A0B的平分线,OD是∠AOC的平分线,且∠BOC+∠COD=75°,求∠BOC和∠COD的度数各是多少度?
如图,0C是∠A0B的平分线,OD是∠AOC的平分线,且∠BOC+∠COD=75°,求∠BOC和∠COD的度数各是多少度?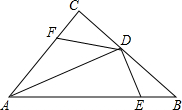 如图,已知:在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,点F在AC上.BD=DF.
如图,已知:在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,点F在AC上.BD=DF.