题目内容
16.某超市用3000元购进某种干果,由于销售状况良好,超市又用9000元第二次购进该干果,但第二次的进价比第一次的提高了20%,第二次购进干果数量是第一次的2倍还多300千克.(1)求该干果的第一次进价是每千克多少元?
(2)百姓超市按每千克9元的价格出售,当大部分干果售出后,余下的按售价的8折售完,若两次销售这种干果的利润不少于5820元,则最多余下多少千克干果按售价的8折销售.
分析 (1)设该种干果的第一次进价是每千克x元,则第二次进价是每千克(1+20%)x元.根据第二次购进干果数量是第一次的2倍还多300千克,列出方程,解方程即可求解.
(2)根据利润=售价-进价列出不等式并解答.
解答 解:(1)设该种干果的第一次进价是每千克x元,则第二次进价是每千克(1+20%)x元,
由题意,得$\frac{9000}{(1+20%)x}$=2×$\frac{3000}{x}$+300,
解得x=5,
经检验x=5是方程的解.
答:该种干果的第一次进价是每千克5元.
(2)设当大部分干果售出后,余下a千克按售价的8折售完,
由题意得:[$\frac{3000}{5}$+$\frac{9000}{5×(1+20%)}$-a]×9+9×80%a-(3000+9000)≥5820,
解得a≤600.
答:当大部分干果售出后,余下的按售价的8折售完,若两次销售这种干果的利润不少于5820元,则最多余下600千克干果按售价的8折销售.
点评 本题考查了分式方程的应用和一元一次不等式的应用.利用分式方程解应用题时,一般题目中会有两个相等关系,这时要根据题目所要解决的问题,选择其中的一个相等关系作为列方程的依据,而另一个则用来设未知数.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
7.下列条件能判断点M是线段AB中点的是( )
| A. | AM=BM | B. | AM=BM=$\frac{1}{2}$AB | C. | AM=$\frac{1}{2}$AB | D. | AM+BM=AB |
11. 如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=3,则PQ的最小值为( )
如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=3,则PQ的最小值为( )
 如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=3,则PQ的最小值为( )
如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=3,则PQ的最小值为( )| A. | 2 | B. | 3 | C. | 4 | D. | 无法确定 |
6.已知扇形的半径为6,圆心角的度数为120°,若将此扇形围成一个圆锥,则围成的圆锥的全面积为( )
| A. | 9π | B. | 12π | C. | 16π | D. | 18π |
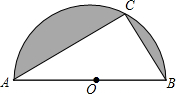 如图,半圆的直径AB,点C在半圆上,已知半径为1,△ABC的周长为$\sqrt{5}$+2,则阴影部分的面积为$\frac{1}{2}π-\frac{1}{4}$.
如图,半圆的直径AB,点C在半圆上,已知半径为1,△ABC的周长为$\sqrt{5}$+2,则阴影部分的面积为$\frac{1}{2}π-\frac{1}{4}$. 如图所示,在Rt△ABC中,∠C=90°,∠BAC=60°,AB=8.半径为$\sqrt{3}$的⊙M与射线BA相切,切点为N,且AN=3.将Rt△ABC顺时针旋转120°后得到Rt△ADE,点B、C的对应点分别是点D、E.此时Rt△ADE的斜边AD所在的直线与⊙M的位置关系是相切.
如图所示,在Rt△ABC中,∠C=90°,∠BAC=60°,AB=8.半径为$\sqrt{3}$的⊙M与射线BA相切,切点为N,且AN=3.将Rt△ABC顺时针旋转120°后得到Rt△ADE,点B、C的对应点分别是点D、E.此时Rt△ADE的斜边AD所在的直线与⊙M的位置关系是相切.