题目内容
11.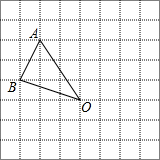 在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABO的三个顶点都在格点上.
在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABO的三个顶点都在格点上.(1)画出△ABO绕点O顺时针旋转90°后的△OA1B1(A的对应点为A1);
(2)直接写出(1)中线段AB扫过的面积为:$\frac{3}{4}$π.
分析 (1)利用网格特点和旋转的性质画出点A、B的对应点A1、B1即可得到△OA1B1;
(2)根据扇形面积公式,利用线段AB扫过的面积=S扇形AOA1+S△ABO-S扇形BOB1-S△A1OB1进行计算.
解答 解:(1)如图,△OA1B1为所作;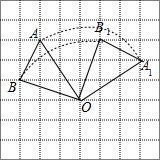
(2)OB=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,OA=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,
线段AB扫过的面积=S扇形AOA1+S△ABO-S扇形BOB1-S△A1OB1
=S扇形AOA1+S△ABO-S扇形BOB1
=$\frac{90•π•(\sqrt{13})^{2}}{360}$-$\frac{90•π•(\sqrt{10})^{2}}{360}$
=$\frac{3}{4}$π.
故答案为$\frac{3}{4}$π.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了扇形的面积公式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.下列命题是真命题的是( )
| A. | 同位角相等 | B. | 平行于同一直线的两条直线平行 | ||
| C. | 点(2,3)在直线y=2x+3上 | D. | 函数y=-x+1中y随x的增大而增大 |
6.已知扇形的半径为6,圆心角的度数为120°,若将此扇形围成一个圆锥,则围成的圆锥的全面积为( )
| A. | 9π | B. | 12π | C. | 16π | D. | 18π |
 用火柴棒按如图所示的方式摆图形,按照这样的规律继续摆下去,用101根火柴棒可以摆出20个六边形.
用火柴棒按如图所示的方式摆图形,按照这样的规律继续摆下去,用101根火柴棒可以摆出20个六边形.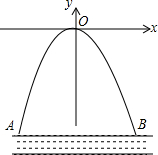 某涵洞是一条抛物线形,它的截面如图所示,现测得水面宽AB=10.6cm,涵洞顶点O到水面的距离为2.4cm,在图中的直角坐标系内,涵洞所在的抛物线的解析式为y=-$\frac{240}{2809}$x2.
某涵洞是一条抛物线形,它的截面如图所示,现测得水面宽AB=10.6cm,涵洞顶点O到水面的距离为2.4cm,在图中的直角坐标系内,涵洞所在的抛物线的解析式为y=-$\frac{240}{2809}$x2.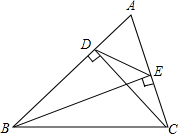 如图,BE,CD是△ABC的两条高.求证:DE•AB=AE•BC.
如图,BE,CD是△ABC的两条高.求证:DE•AB=AE•BC.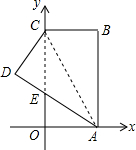 如图,在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(4,8),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E,那么点D的坐标为(-$\frac{12}{5}$,$\frac{24}{5}$).
如图,在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(4,8),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E,那么点D的坐标为(-$\frac{12}{5}$,$\frac{24}{5}$).