题目内容
1.方程|$\frac{x-1}{2}$|+|$\frac{1-x}{3}$|=0的解是( )| A. | 1 | B. | 无数个 | C. | 0 | D. | 无解 |
分析 分类讨论:x<1,x≥1,根据绝对值的性质,可化简绝对值,根据解一元一次方程的一般步骤,可得答案.
解答 解:①当x<1时,原方程化简得$\frac{1-x}{2}$+$\frac{1-x}{3}$=0,
去分母,得3(1-x)+2(1-x)=0,
去括号,得3-3x+2-2x=0,
移项,得-3x-2x=-3-2,
合并同类项,得-5x=-5,
系数化为1,得x=1(不符合题意的解要舍去);
②当x≥1时,原方程化简得$\frac{x-1}{2}$+$\frac{x-1}{3}$=0,
去分母,得3(x-1)+2(x-1)=0,
去括号,得3x-3+2x-2=0,
移项,得3x+2x=3+2,
合并同类项,得5x=5,
系数化为1,得x=1,
综上所述:x=1是方程的解.
故选:A.
点评 本题考查了含绝对值符号的一元一次方程,利用绝对值的性质化简方程是解题关键,要分类讨论,以防遗漏.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
11. 如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=3,则PQ的最小值为( )
如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=3,则PQ的最小值为( )
 如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=3,则PQ的最小值为( )
如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=3,则PQ的最小值为( )| A. | 2 | B. | 3 | C. | 4 | D. | 无法确定 |
12.若x2+(m-3)x+16是完全平方式,则m的值是( )
| A. | 11 | B. | -5 | C. | ±8 | D. | 11或-5 |
9.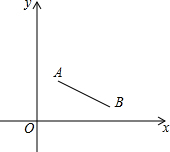 如图,点A、B的坐标分别为(1,2),(3,$\frac{1}{2}$),现将线段AB绕点B顺时针旋转180°得线段A1B,则A1的坐标为( )
如图,点A、B的坐标分别为(1,2),(3,$\frac{1}{2}$),现将线段AB绕点B顺时针旋转180°得线段A1B,则A1的坐标为( )
 如图,点A、B的坐标分别为(1,2),(3,$\frac{1}{2}$),现将线段AB绕点B顺时针旋转180°得线段A1B,则A1的坐标为( )
如图,点A、B的坐标分别为(1,2),(3,$\frac{1}{2}$),现将线段AB绕点B顺时针旋转180°得线段A1B,则A1的坐标为( )| A. | (1,-5) | B. | (5,-2) | C. | (5,-1) | D. | (-1,5) |
6.已知扇形的半径为6,圆心角的度数为120°,若将此扇形围成一个圆锥,则围成的圆锥的全面积为( )
| A. | 9π | B. | 12π | C. | 16π | D. | 18π |
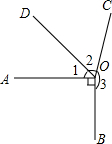 (1)从点O引四条射线OA,OB,OC,OD,如果∠AOB:∠BOC:∠COD:∠DOA=1:2:3:4,那么这四个角的度数分别是多少?
(1)从点O引四条射线OA,OB,OC,OD,如果∠AOB:∠BOC:∠COD:∠DOA=1:2:3:4,那么这四个角的度数分别是多少?
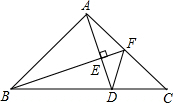 △ABC中,∠BAC=90°,AB=AC,F为AC中点,连接BF作AE⊥BF交BF于E,交BC于D,求证:∠AFB=∠CFD.
△ABC中,∠BAC=90°,AB=AC,F为AC中点,连接BF作AE⊥BF交BF于E,交BC于D,求证:∠AFB=∠CFD.