题目内容
14.已知关于x的方程(x-3)(x-2)-p2=0.(1)求证:方程总有两个不相等的实数根.
(2)设方程的两根为x1,x2(x1<x2),则当0≤p$<\sqrt{6}$时,请直接写出x1和x2的取值范围.
分析 (1)方程整理为一般形式,表示出根的判别式,根据根的判别式的值为正数,即可得证;
(2)根据p的范围,表示出两根的取值范围即可.
解答 (1)证明:方程可变形为x2-5x+6-p2=0,
∵△=25-4(6-p2)=4p2+1>0,
∴方程总有两个不相等的实数根;
(2)解:设方程的两根为x1,x2(x1<x2),
则当0≤p$<\sqrt{6}$时,x1和x2的取值范围分别为0<x1≤2,3≤x2<5.
点评 此题考查了根的判别式,以及根与系数的关系,熟练掌握运算法则是解本题的关键.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
9.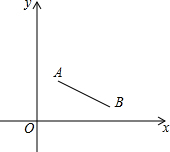 如图,点A、B的坐标分别为(1,2),(3,$\frac{1}{2}$),现将线段AB绕点B顺时针旋转180°得线段A1B,则A1的坐标为( )
如图,点A、B的坐标分别为(1,2),(3,$\frac{1}{2}$),现将线段AB绕点B顺时针旋转180°得线段A1B,则A1的坐标为( )
 如图,点A、B的坐标分别为(1,2),(3,$\frac{1}{2}$),现将线段AB绕点B顺时针旋转180°得线段A1B,则A1的坐标为( )
如图,点A、B的坐标分别为(1,2),(3,$\frac{1}{2}$),现将线段AB绕点B顺时针旋转180°得线段A1B,则A1的坐标为( )| A. | (1,-5) | B. | (5,-2) | C. | (5,-1) | D. | (-1,5) |
19.下列命题是真命题的是( )
| A. | 同位角相等 | B. | 平行于同一直线的两条直线平行 | ||
| C. | 点(2,3)在直线y=2x+3上 | D. | 函数y=-x+1中y随x的增大而增大 |
6.已知扇形的半径为6,圆心角的度数为120°,若将此扇形围成一个圆锥,则围成的圆锥的全面积为( )
| A. | 9π | B. | 12π | C. | 16π | D. | 18π |
 如图所示,在Rt△ABC中,∠C=90°,∠BAC=60°,AB=8.半径为$\sqrt{3}$的⊙M与射线BA相切,切点为N,且AN=3.将Rt△ABC顺时针旋转120°后得到Rt△ADE,点B、C的对应点分别是点D、E.此时Rt△ADE的斜边AD所在的直线与⊙M的位置关系是相切.
如图所示,在Rt△ABC中,∠C=90°,∠BAC=60°,AB=8.半径为$\sqrt{3}$的⊙M与射线BA相切,切点为N,且AN=3.将Rt△ABC顺时针旋转120°后得到Rt△ADE,点B、C的对应点分别是点D、E.此时Rt△ADE的斜边AD所在的直线与⊙M的位置关系是相切. 用火柴棒按如图所示的方式摆图形,按照这样的规律继续摆下去,用101根火柴棒可以摆出20个六边形.
用火柴棒按如图所示的方式摆图形,按照这样的规律继续摆下去,用101根火柴棒可以摆出20个六边形.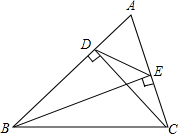 如图,BE,CD是△ABC的两条高.求证:DE•AB=AE•BC.
如图,BE,CD是△ABC的两条高.求证:DE•AB=AE•BC.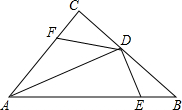 如图,已知:在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,点F在AC上.BD=DF.
如图,已知:在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,点F在AC上.BD=DF.