题目内容
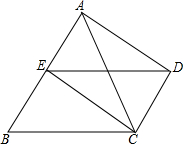 已知,如图,△ABC中,E为AB的中点,DC∥AB,且DC=
已知,如图,△ABC中,E为AB的中点,DC∥AB,且DC=| 1 |
| 2 |
(1)求证:△AED≌△EBC;
(2)请对△ABC添加一个条件:
(3)请对△ABC添加一个条件:
考点:菱形的判定,全等三角形的判定与性质,矩形的判定
专题:
分析:(1)由DC∥AB,且DC=
AB,E为AB的中点,可判定四边形ADCE是平行四边形,得出AD=EC,AD∥CE,根据两直线平行同位角相等得出∠BEC=∠BAD,再利用SAS即可证得△BEC≌△EAD;
(2)添加一个条件:BC=AC,可使得四边形AECD成为矩形.由CD=BE且CD∥BE,可得四边形BCDE是平行四边形,得出BC=DE,由BC=AC,等量代换得到DE=AC,由(1)可知四边形ADCE是平行四边形,根据对角线相等的平行四边形是矩形可得四边形AECD是矩形;
(3)添加一个条件:AB=2BC,可使得四边形BCDE成为菱形.由E为AB的中点,AB=2BC,可得BE=BC,而四边形BCDE是平行四边形,根据邻边相等的平行四边形是菱形可得四边形BCDE是菱形.
| 1 |
| 2 |
(2)添加一个条件:BC=AC,可使得四边形AECD成为矩形.由CD=BE且CD∥BE,可得四边形BCDE是平行四边形,得出BC=DE,由BC=AC,等量代换得到DE=AC,由(1)可知四边形ADCE是平行四边形,根据对角线相等的平行四边形是矩形可得四边形AECD是矩形;
(3)添加一个条件:AB=2BC,可使得四边形BCDE成为菱形.由E为AB的中点,AB=2BC,可得BE=BC,而四边形BCDE是平行四边形,根据邻边相等的平行四边形是菱形可得四边形BCDE是菱形.
解答:(1)证明:∵DC=
AB,E为AB的中点,
∴CD=BE=AE.
又∵DC∥AB,
∴四边形ADCE是平行四边形,
∴AD=EC,AD∥CE,
∴∠BEC=∠BAD.
在△BEC和△EAD中,
,
∴△BEC≌△EAD(SAS);
(2)解:添加一个条件:BC=AC,可使得四边形AECD成为矩形;
(3)解:添加一个条件:AB=2BC,可使得四边形BCDE成为菱形.
∵E为AB的中点,
∴AB=2BE,
∵AB=2BC,
∴BE=BC,
∵CD=BE且CD∥BE,
∴四边形BCDE是平行四边形,
∴四边形BCDE是菱形.
故答案为BC=AC;AB=2BC.
| 1 |
| 2 |
∴CD=BE=AE.
又∵DC∥AB,
∴四边形ADCE是平行四边形,
∴AD=EC,AD∥CE,
∴∠BEC=∠BAD.
在△BEC和△EAD中,
|
∴△BEC≌△EAD(SAS);
(2)解:添加一个条件:BC=AC,可使得四边形AECD成为矩形;
(3)解:添加一个条件:AB=2BC,可使得四边形BCDE成为菱形.
∵E为AB的中点,
∴AB=2BE,
∵AB=2BC,
∴BE=BC,
∵CD=BE且CD∥BE,
∴四边形BCDE是平行四边形,
∴四边形BCDE是菱形.
故答案为BC=AC;AB=2BC.
点评:本题考查了全等三角形的性质和判定,矩形、菱形的判定,平行四边形的判定与性质,主要考查学生的推理能力,注意:对角线相等的平行四边形是矩形,有一组邻边相等的平行四边形是菱形.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
将抛物线y=2x2-4x-5向上平移6个单位长度,再向左平移2个单位长度,最后所得抛物线绕原点转180°,得到新的抛物线解析式( )
| A、y=2x2-4x-5 |
| B、y=-2x2+4x-1 |
| C、y=2x2+12x+19 |
| D、y=-2x2-12x-17 |
已知二次函数y=3x2-6x+5,若它的顶点不动,把开口反向,再沿对称轴平移,得到一条新抛物线,它恰好与直线y=mx-2交于点(2,4),则新抛物线的解析式为( )
| A、y=3x2+6x-4 |
| B、y=3x2+6x+4 |
| C、y=3x2-6x+4 |
| D、y=6x2-3x+4 |
 校门口经常有人搞摸奖.在一只黑色的口袋里装有处颜色外都相同的50只小球,其中红球1只,黄球2只,绿球10只,其余为白球.搅拌均匀后,任意摸1个球.奖品的情况标注在球上.
校门口经常有人搞摸奖.在一只黑色的口袋里装有处颜色外都相同的50只小球,其中红球1只,黄球2只,绿球10只,其余为白球.搅拌均匀后,任意摸1个球.奖品的情况标注在球上.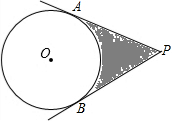 如图,已知PA、PB切⊙O于A、B两点,PO=4cm,∠APB=60°,求阴影部分的周长.
如图,已知PA、PB切⊙O于A、B两点,PO=4cm,∠APB=60°,求阴影部分的周长.