题目内容
 校门口经常有人搞摸奖.在一只黑色的口袋里装有处颜色外都相同的50只小球,其中红球1只,黄球2只,绿球10只,其余为白球.搅拌均匀后,任意摸1个球.奖品的情况标注在球上.
校门口经常有人搞摸奖.在一只黑色的口袋里装有处颜色外都相同的50只小球,其中红球1只,黄球2只,绿球10只,其余为白球.搅拌均匀后,任意摸1个球.奖品的情况标注在球上.(1)如果花2元摸1个球,那么摸不到奖的概率是多少?
(2)如果花4元同时摸2个球,那么奖得奖品价值超过4元的概率是多少?
考点:列表法与树状图法
专题:计算题
分析:(1)求出摸到白球的概率,即为摸不到奖的概率;
(2)求出摸出奖品为两个2元的概率,再由1减去此概率,再减去无奖的概率,求出奖得奖品价值超过4元的概率即可.
(2)求出摸出奖品为两个2元的概率,再由1减去此概率,再减去无奖的概率,求出奖得奖品价值超过4元的概率即可.
解答:解:(1)根据题意得:白球个数为50-(1+2+10)=37(个),
则P(摸不到奖)=
;
(2)若摸出两个为绿球的概率为
=
,
则P(奖得奖品价值超过4元)=1-
-
=
.
则P(摸不到奖)=
| 37 |
| 50 |
(2)若摸出两个为绿球的概率为
| 10×10 |
| 50×50 |
| 1 |
| 25 |
则P(奖得奖品价值超过4元)=1-
| 1 |
| 25 |
| 37 |
| 50 |
| 11 |
| 50 |
点评:此题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目

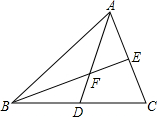 如图,△ABC中,AB=BC,AC=8,点F是△ABC的重心(即点F是△ABC的两条中线AD、BE的交点),BF=6,则DF=
如图,△ABC中,AB=BC,AC=8,点F是△ABC的重心(即点F是△ABC的两条中线AD、BE的交点),BF=6,则DF=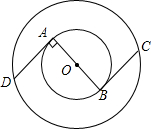 如图,在两个同心圆⊙O中,AB是小圆的直径,BC与小圆相切于点B,并交大圆于点C,且BC=
如图,在两个同心圆⊙O中,AB是小圆的直径,BC与小圆相切于点B,并交大圆于点C,且BC=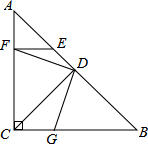 已知在△ABC中,∠ACB=90°,AC=BC,CD⊥AB,垂足为D,E是AB上一点,EF⊥AC,垂足为F,G是BC上一点,CG=EF,求证:DF=DG.
已知在△ABC中,∠ACB=90°,AC=BC,CD⊥AB,垂足为D,E是AB上一点,EF⊥AC,垂足为F,G是BC上一点,CG=EF,求证:DF=DG.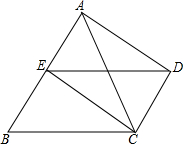 已知,如图,△ABC中,E为AB的中点,DC∥AB,且DC=
已知,如图,△ABC中,E为AB的中点,DC∥AB,且DC=