题目内容
AE,BD是锐角△ABC的两条高,如果S△ABC=18,S△DCE=2,求
= .
| DE |
| AB |
考点:三角形的面积
专题:
分析:首先证明△BDC∽△AEC,由相似三角形的性质可得DC:BC=EC:AC,又因为∠ACB=∠ECD,所以△DEC∽△BAC,由面积之比可得到对应边之比即
=(
)2,利用相似的性质即可求出
的值.
| S△DEC |
| S△ABC |
| DE |
| AB |
| DE |
| AB |
解答: 解:连接DE
解:连接DE
∵∠C是公共角,∠BDC=∠AEC=90°,
∴△BDC∽△AEC,
∴DC:BC=EC:AC,
∴△DEC∽△BAC,
∴
=(
)2,
∵S△ABC:S△DEC=9,
∴两个三角形的边长之比为3:1,
∴DE:AB=1:3,
故答案为
.
 解:连接DE
解:连接DE∵∠C是公共角,∠BDC=∠AEC=90°,
∴△BDC∽△AEC,
∴DC:BC=EC:AC,
∴△DEC∽△BAC,
∴
| S△DEC |
| S△ABC |
| DE |
| AB |
∵S△ABC:S△DEC=9,
∴两个三角形的边长之比为3:1,
∴DE:AB=1:3,
故答案为
| 1 |
| 3 |
点评:本题考查了相似三角形的判定和性质,在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用.

练习册系列答案
相关题目
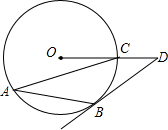 如图,AB、AC是⊙O的两条弦,过点B的切线与OC的延长线交于点D,若∠D=36°,则∠CAB的度数为( )
如图,AB、AC是⊙O的两条弦,过点B的切线与OC的延长线交于点D,若∠D=36°,则∠CAB的度数为( )| A、54° | B、44° |
| C、27° | D、22° |
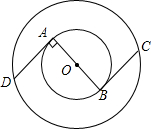 如图,在两个同心圆⊙O中,AB是小圆的直径,BC与小圆相切于点B,并交大圆于点C,且BC=
如图,在两个同心圆⊙O中,AB是小圆的直径,BC与小圆相切于点B,并交大圆于点C,且BC=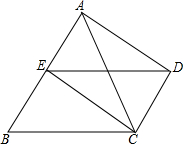 已知,如图,△ABC中,E为AB的中点,DC∥AB,且DC=
已知,如图,△ABC中,E为AB的中点,DC∥AB,且DC=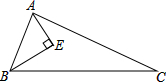 如图所示,在△ABC中,AE平分∠BAC,BE⊥AE,∠ABE=2∠C,求证:AC-AB=2BE.
如图所示,在△ABC中,AE平分∠BAC,BE⊥AE,∠ABE=2∠C,求证:AC-AB=2BE.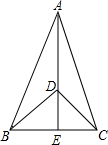 如图,在△ABC中,AB=AC,∠ABD=∠ACD,AD的延长线交BC于E.
如图,在△ABC中,AB=AC,∠ABD=∠ACD,AD的延长线交BC于E.