题目内容
3.结合数轴与绝对值的知识解答下列问题:(1)数轴上表示3和2两点间的距离是1;
表示-3和2两点间的距离是5;
一般地,数轴上表示数m和n两点间的距离=|m-n|;
(2)如果在数轴上表示数a的点与-2的距离是3,那么a=-5或1;
(3)如果数轴上表示数a的点位于-4和2之间,求|a+4|+|a-2|的值;
(4)当a取何值时,|a+5|+|a-1|+|a-4|的值最小,最小值为多少?请说明理由;
(5)直接回答:当式子|a+9|+|a+1|+|a-5|+|a-7|取最小值时,相应的a取值范围是什么?最小值是多少?
分析 (1)根据两点间的距离公式,可得答案;
(2)根据两点间的距离公式可得|a+2|=3,解方程可得答案;
(3)先计算绝对值,再合并同类项即可求解;
(4)根据线段上的点到线段两端点的距离的和最小,可得答案;
(5)根据线段上的点到线段两端点的距离的和最小,可得答案.
解答 解:(1)数轴上表示3和2两点间的距离是3-2=1;
表示-3和2两点间的距离是2-(-3)=5;
一般地,数轴上表示数m和n两点间的距离=|m-n|;
(2)依题意有
|a+2|=3,
解得a=-5或1;
(3)∵数轴上表示数a的点位于-4和2之间,
∴|a+4|+|a-2|
=a+4-a+2
=6;
(4)因为|a+5|+|a-4|最小值为4-(-5)=9,|a-1|是非负数
所以当a=1时,
|a+5|+|a-1|+|a-4|
=6+0+3
=9;
(5)|a+9|+|a+1|+|a-5|+|a-7|取最小值时,相应的a取值范围是-1≤x≤5,
最小值是a+9+a+1-a+5-a+7=22.
故答案为:1,5,|m-n|;-5或1.
点评 本题考查了绝对值,利用了两点间的距离公式,注意线段上的点与线段两端点的距离的和最小.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.如果4a2+1与一个单项式的和恰好是一个整式的平方,那么这样的单项式共有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 5个 |
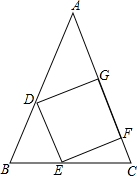 已知,如图,正方形DEFG的一边FG在等腰△ABC的腰AC上,AB=AC=5,顶点D、E分别为边AB、BC上,△ABC的面积为10,求正方形DEFG的面积.
已知,如图,正方形DEFG的一边FG在等腰△ABC的腰AC上,AB=AC=5,顶点D、E分别为边AB、BC上,△ABC的面积为10,求正方形DEFG的面积.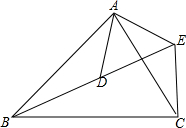 如图,AB:AD=BC:DE=AC:AE.
如图,AB:AD=BC:DE=AC:AE.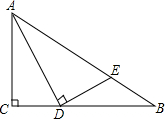 如图,在Rt△ABC中,∠C=90°,点D在边BC上,过点D作DE⊥AD交AB于点E,且DE=BE.
如图,在Rt△ABC中,∠C=90°,点D在边BC上,过点D作DE⊥AD交AB于点E,且DE=BE. 如图,轮船B在灯塔A北偏东40°方向,轮船C在轮船B南偏东40°方向,如果∠ABC=∠C.通过计算说明轮船C在灯塔A的什么方向?
如图,轮船B在灯塔A北偏东40°方向,轮船C在轮船B南偏东40°方向,如果∠ABC=∠C.通过计算说明轮船C在灯塔A的什么方向?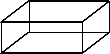 一个无盖长方体盒子的容积是V.
一个无盖长方体盒子的容积是V.