题目内容
13.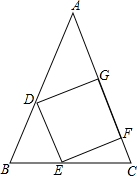 已知,如图,正方形DEFG的一边FG在等腰△ABC的腰AC上,AB=AC=5,顶点D、E分别为边AB、BC上,△ABC的面积为10,求正方形DEFG的面积.
已知,如图,正方形DEFG的一边FG在等腰△ABC的腰AC上,AB=AC=5,顶点D、E分别为边AB、BC上,△ABC的面积为10,求正方形DEFG的面积.
分析 过B作BH⊥AC于H,交DE于M,根据已知条件求得BH=4,通过△BDE∽△BAC,得到$\frac{DE}{AC}=\frac{BM}{BH}$,求得DE=$\frac{20}{9}$,于是得到结果.
解答  解:过B作BH⊥AC于H,交DE于M,
解:过B作BH⊥AC于H,交DE于M,
∵△ABC的面积为10,AB=AC=5,
∴BH=4,
∵四边形DEFG是正方形,
∴DE∥AC,
∴△BDE∽△BAC,
∴$\frac{DE}{AC}=\frac{BM}{BH}$,
∴DE=$\frac{20}{9}$,
∴正方形DEFG的面积=$\frac{400}{81}$.
点评 本题考查了相似三角形的判定和性质,正方形的性质和面积,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
4.下表是2007-2011年中国数字音乐销售额统计表:
(1)请根据表中数据,建立平面直角坐标系.并描出坐标(年份,中国数字音乐销售额);
(2)试用直线表示我国数字音乐市场规模在近几年内的发展趋势.
| 年份 | 2007 | 2008 | 2009 | 2010 | 2011 |
| 中国数字音乐销售额/亿元 | 15.2 | 16.5 | 17.9 | 19.5 | 21.5 |
(2)试用直线表示我国数字音乐市场规模在近几年内的发展趋势.
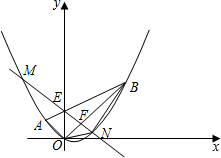 如图,平面直角坐标系xOy中,点A的坐标为(-2,2),点B的坐标为(6,6),抛物线经过A、O、B三点,连结OA、OB、AB,线段AB交y轴于点E.
如图,平面直角坐标系xOy中,点A的坐标为(-2,2),点B的坐标为(6,6),抛物线经过A、O、B三点,连结OA、OB、AB,线段AB交y轴于点E.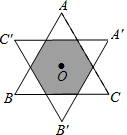 如图,已知等边三角形的面积为1,O为△ABC的中心(O到△ABC的各边距离相等),将△ABC绕中心O旋转60°,得到△A′B′C′,则△ABC与△A′B′C′重叠部分的面积为$\frac{2}{3}$.
如图,已知等边三角形的面积为1,O为△ABC的中心(O到△ABC的各边距离相等),将△ABC绕中心O旋转60°,得到△A′B′C′,则△ABC与△A′B′C′重叠部分的面积为$\frac{2}{3}$. 某块试验田里的农作物每天的需水量y(千克)与生长时间x(天)之间的关系如折线图所示.这些农作物在第10天、30天的需水量分别为2000千克、3000千克,在第40天后每天的需水量比前一天增加100千克.
某块试验田里的农作物每天的需水量y(千克)与生长时间x(天)之间的关系如折线图所示.这些农作物在第10天、30天的需水量分别为2000千克、3000千克,在第40天后每天的需水量比前一天增加100千克.