题目内容
13.如果方程(k-1)x2-(2k-1)x+k-3=0有两个实数根,求k的取值范围.分析 由方程(k-1)x2-(2k-1)x+k-3=0有两个实数根,可得△≥0且k-1≠0,即可求得k的取值范围.
解答 解:∵方程(k-1)x2-(2k-1)x+k-3=0有两个实数根,
∴△=b2-4ac=[-(2k-1)]2-4(k-1)(k-3)=12k-11≥0,
解得:k≥$\frac{11}{12}$,
∵k-1≠0,
∴k≠1,
∴k的取值范围为:k≥$\frac{11}{12}$且k≠0.
点评 此题考查了根的判别式.注意当△≥0是,方程有两个实数根.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
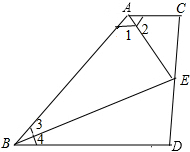 如图,AD∥BC,∠1=∠2,E为CD的中点,求证:∠3=∠4.
如图,AD∥BC,∠1=∠2,E为CD的中点,求证:∠3=∠4.