题目内容
12.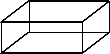 一个无盖长方体盒子的容积是V.
一个无盖长方体盒子的容积是V.(1)若盒子地面边长为a的正方形,则这个盒子的外表面积S1=a2+$\frac{4V}{a}$(盒子各个面的厚度忽略不计,下同)
(2)若盒子底面是长为b,宽为c的长方形,则这个盒子的外表面积S2=bc+$\frac{2V(b+c)}{bc}$
(3)在(1)和(2)中,如果盒子的底面积相等,那么这两个盒子的外表面积之差:S2-S1=$\frac{2V(2a-b-c)}{{a}^{2}}$.
分析 (1)利用长方体体积公式表示出长方体的高,进而得出其表面积;
(2)利用长方体体积公式表示出长方体的高,进而得出其表面积;
(3)利用(1),(2)中所求,进而计算得出答案.
解答 解:(1)∵一个无盖长方体盒子的容积是V,盒子地面边长为a的正方形,
∴长方体盒子的高为:h=$\frac{V}{{a}^{2}}$,
∴这个盒子的外表面积S1=a2+$\frac{V}{{a}^{2}}$×4a=a2+$\frac{4V}{a}$;
故答案为:a2+$\frac{4V}{a}$;
(2)∵一个无盖长方体盒子的容积是V,盒子底面是长为b,宽为c的长方形,
∴长方体盒子的高为:h=$\frac{V}{bc}$,
∴这个盒子的外表面积S2=bc+$\frac{V}{bc}$×2(b+c)=bc+$\frac{2V(b+c)}{bc}$;
故答案为:bc+$\frac{2V(b+c)}{bc}$;
(3)∵盒子的底面积相等,
∴a2=bc,
∴这两个盒子的外表面积之差:
S2-S1=a2+$\frac{4V}{a}$-(bc+$\frac{2V(b+c)}{bc}$)
=a2+$\frac{4V}{a}$-(a2+$\frac{2V(b+c)}{{a}^{2}}$)
=$\frac{4Va-2V(b+c)}{{a}^{2}}$
=$\frac{2V(2a-b-c)}{{a}^{2}}$.
故答案为:$\frac{2V(2a-b-c)}{{a}^{2}}$.
点评 此题主要考查了列代数式,根据长方体体积得出其高度是解题关键.

练习册系列答案
相关题目
 如图,C为△ABE的边BE上,且AB=AC,AB的垂直平分线交AC于D,且AD=BC,CE=CD.
如图,C为△ABE的边BE上,且AB=AC,AB的垂直平分线交AC于D,且AD=BC,CE=CD.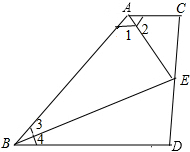 如图,AD∥BC,∠1=∠2,E为CD的中点,求证:∠3=∠4.
如图,AD∥BC,∠1=∠2,E为CD的中点,求证:∠3=∠4.