Question

18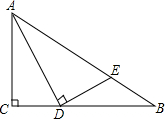．如图，在Rt△ABC中，∠C=90°，点D在边BC上，过点D作DE⊥AD交AB于点E，且DE=BE．
（1）求证：△ABC∽△DAC；
（2）若AD²=AC•AE，求证：BD=2CD．

Answer 1

分析 （1）根据等腰三角形的性质得到∠EDB=∠B，由余角的性质得到∠BAC=∠ADC，由于∠C=∠C，于是得到△ABC∽△DAC；
（2）由已知条件得到$\frac{AD}{AC}=\frac{AC}{AE}$，推出R_t△ACD∽R_t△ADE，得到∠CAD=∠DAE，求得∠DAE=∠B=∠CAD=30°，根据等腰三角形的性质和直角三角形的性质得到AD=BD，CD=$\frac{1}{2}$AD，即可得到结论．

解答 解：（1）∵DE=BE，
∴∠EDB=∠B，
∵∠C=90°，DE⊥AD，
∴∠BAC+∠B=∠ADC+∠EDB，
∴∠BAC=∠ADC，
∵∠C=∠C，
∴△ABC∽△DAC；

（2）∵AD²=AC•AE，
∴$\frac{AD}{AC}=\frac{AC}{AE}$，
∴R_t△ACD∽R_t△ADE，
∴∠CAD=∠DAE，
∵∠DAE=∠B，∠DAE+∠B+∠CAD=90°，
∴∠DAE=∠B=∠CAD=30°，
∴AD=BD，CD=$\frac{1}{2}$AD，
∴BD=2CD．

点评 本题考查了相似三角形的判定和性质，等腰三角形的性质，直角三角形的性质，熟练掌握相似三角形的判定和性质是解题的关键．