题目内容
13.用若干火柴首尾相接摆成一个长方形,设一根火柴的长度为1,长方形的两邻边的长分别为x,y,要求摆成的长方形的面积为18.(1)求y关于x的函数解析式和自变量的取值范围;
(2)用这些火柴且火柴全部用完能否摆成正方形?请说明理由.
分析 (1)直接利用长方形面积得出y与x之间的关系;
(2)利用正方形的性质得出其边长进而得出答案.
解答 解:(1)由题意可得:xy=18,
则y=$\frac{18}{x}$(1≤x≤18);
(2)不能摆成正方形,
理由:当正方形的面积为18,则其边长为:3$\sqrt{2}$,
∵一根火柴的长度为1,
∴其边长不可能围成3$\sqrt{2}$.
点评 此题主要考查了放比例函数的应用,正确得出y与x之间的关系是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.已知关于x的方程ax2+bx+c=0的两根分别为-3和1,则方程bx2+cx+a=0的两根为( )
| A. | -$\frac{1}{3}$和1 | B. | $\frac{1}{2}$和1 | C. | $\frac{1}{3}$和-1 | D. | -$\frac{1}{2}$和-1 |
18. 如图,在5×5的正方形网格中,线段AB的长度与下列哪个整数最接近( )
如图,在5×5的正方形网格中,线段AB的长度与下列哪个整数最接近( )
 如图,在5×5的正方形网格中,线段AB的长度与下列哪个整数最接近( )
如图,在5×5的正方形网格中,线段AB的长度与下列哪个整数最接近( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
10.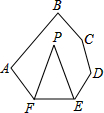 如图,在六边形ABCDEF中,∠A+∠B+∠C+∠D=460°,FP、EP分别平分∠AFE,∠FED,则∠P的度数是( )
如图,在六边形ABCDEF中,∠A+∠B+∠C+∠D=460°,FP、EP分别平分∠AFE,∠FED,则∠P的度数是( )
 如图,在六边形ABCDEF中,∠A+∠B+∠C+∠D=460°,FP、EP分别平分∠AFE,∠FED,则∠P的度数是( )
如图,在六边形ABCDEF中,∠A+∠B+∠C+∠D=460°,FP、EP分别平分∠AFE,∠FED,则∠P的度数是( )| A. | 50° | B. | 55° | C. | 60° | D. | 65° |

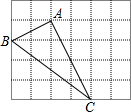 如图,正方形网格中的△ABC,若小方格边长为1,请你根据所学的知识解决下列问题.
如图,正方形网格中的△ABC,若小方格边长为1,请你根据所学的知识解决下列问题.