题目内容
5．
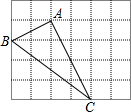如图，正方形网格中的△ABC，若小方格边长为1，请你根据所学的知识解决下列问题．（1）求△ABC的面积；
（2）判断△ABC是什么形状，并说明理由．
分析 （1）运用割补法，正方形的面积减去三个小三角形的面积，即可求出△ABC的面积；
（2）根据勾股定理求得△ABC各边的长，再利用勾股定理的逆定理进行判定，从而不难得到其形状．
解答 解：（1）△ABC的面积=4×4-1×2÷2-4×3÷2-2×4÷2=16-1-6-4=5，
故△ABC的面积为5；
（2）∵小方格边长为1，
∴AB2=12+22=5，AC2=22+42=20，BC2=32+42=25，
∴AB2+AC2=BC2，
∴△ABC为直角三角形．
点评 本题主要考查了勾股定理和勾股定理的逆定理，解答此题要运用勾股定理的逆定理：若三角形ABC的三边满足a2+b2=c2，则三角形ABC是直角三角形．
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
20．点A（a，b），B（a-1，c），其中a＜0，且b＜c，则A，B两点可能在下列（ ）函数的图象上．
| A． | y=2x+3 | B． | y=-$\frac{3}{x}$ | C． | y=$\frac{2}{x}$ | D． | y=$\frac{3}{x}$（x＞0） |
2．双曲线y=$\frac{k}{x}$（k＜0）上有A、B两点且A、B在同一象限，直线AB交y轴于点D，交x轴于点C，且OC=OD，若A（-$\frac{4}{3}$，1），则点B的坐标为（ ）
| A． | （-1，$\frac{4}{3}$） | B． | （-1，$\frac{3}{4}$） | C． | （-1，$\frac{2}{3}$） | D． | （-1，$\frac{3}{2}$） |