题目内容
10．
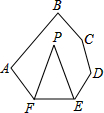如图，在六边形ABCDEF中，∠A+∠B+∠C+∠D=460°，FP、EP分别平分∠AFE，∠FED，则∠P的度数是（ ）| A． | 50° | B． | 55° | C． | 60° | D． | 65° |
分析 首先求得六边形的内角和，则∠AFE与∠DEF的和即可求得，然后根据角平分线的定义求得∠PEF+∠PFE，然后在△PEF中利用三角形内角和定理求解．
解答 解：六边形的内角和是：（6-2）×180°=720°，
则∠PEF+∠PFE=720°-（∠A+∠B+∠C+∠D）=720°-460°=260°，
∵FP、EP分别平分∠AFE，∠FED，
∠PEF+∠PFE=$\frac{1}{2}$（∠PEF+∠PFE）=$\frac{1}{2}$×260°=130°，
在△PEF中，∠P=180°-（∠PEF+∠PFE）=180°-130°=50°．
故选A．
点评 本题考查了多边形的内角和定理，以及角平分线的定义，正确求得∠PEF+∠PFE是关键．
练习册系列答案
相关题目
2．双曲线y=$\frac{k}{x}$（k＜0）上有A、B两点且A、B在同一象限，直线AB交y轴于点D，交x轴于点C，且OC=OD，若A（-$\frac{4}{3}$，1），则点B的坐标为（ ）
| A． | （-1，$\frac{4}{3}$） | B． | （-1，$\frac{3}{4}$） | C． | （-1，$\frac{2}{3}$） | D． | （-1，$\frac{3}{2}$） |
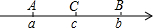如图，已知数轴上点A，B，C所对应的数a，b，c都不为0，且C是AB的中点，如果|a+b|-|a-2c|+|b-2c|-|a+b-2c|=0，试确定原点O的大致位置．