题目内容
1.已知直角三角形的两条直角边a、b(a≤b)及斜边c均为整数,且其内切圆的半径r=3.则这样的直角三角形有( )个.| A. | 0 | B. | 1 | C. | 3 | D. | 无数个 |
分析 根据三角形内切圆的性质可得出a-3+b-3=c,再由勾股定理得出a2+b2=c2,化简整理即可得出a,b的值,再求得c的对应值.
解答 解:∵三角形内切圆的半径r=3,
∴a-r+b-r=c,
∴a+b-c=2r=6,
∵直角三角形的两条直角边a、b(a≤b)及斜边c均为整数,
∴a2+b2=c2,
∴a2+b2=(a+b-6)2,
∴(a-6)(b-6)=18,
∵a、b、c均为正整数,且a≤b,
∴可得$\left\{\begin{array}{l}{a-6=1}\\{b-6=18}\end{array}\right.$或$\left\{\begin{array}{l}{a-6=2}\\{b-6=9}\end{array}\right.$或$\left\{\begin{array}{l}{a-6=3}\\{b-6=6}\end{array}\right.$,
可解出$\left\{\begin{array}{l}{a=7}\\{b=24}\end{array}\right.$或$\left\{\begin{array}{l}{a=8}\\{b=15}\end{array}\right.$或$\left\{\begin{array}{l}{a=9}\\{b=12}\end{array}\right.$,
∴对应的c分别为25,17,15,
∴满足条件的直角三角形有3个.
故选C.
点评 本题考查了三角形的内切圆与内心,以及非一次不定方程及勾股定理,解答此题的关键是先利用勾股定理把原式化为两个因式积的形式,再根据a,b均为正整数进行解答.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
20.下列数据具有一定的排列规律:

若整数2016位于第a行,从左数第b个数,则a+b的值是( )

若整数2016位于第a行,从左数第b个数,则a+b的值是( )
| A. | 63 | B. | 126 | C. | 2015 | D. | 1002 |
17.为丰富学生课余活动,某校开展校园艺术节十佳歌手比赛,共有18名同学入围,他们的决赛成绩如表:
则入围同学决赛成绩的中位数和众数分别是( )
| 成绩(分) | 9.40 | 9.50 | 9.60 | 9.70 | 9.80 | 9.90 |
| 人数 | 2 | 3 | 5 | 4 | 3 | 1 |
| A. | 9.70,9.60 | B. | 9.60,9.60 | C. | 9.60,9.70 | D. | 9.65,9.60 |
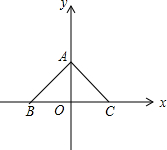 如图,在直角坐标平面内有两点A(0,2)、B(-2,0)、C(2,0).
如图,在直角坐标平面内有两点A(0,2)、B(-2,0)、C(2,0). 如图,在△ABC中,AB=AC,AD是BC边上的中线,AE⊥BE于点E,且BE=$\frac{1}{2}BC$.
如图,在△ABC中,AB=AC,AD是BC边上的中线,AE⊥BE于点E,且BE=$\frac{1}{2}BC$.