题目内容
11．先化简再计算：$\frac{{\sqrt{a+b}}}{{\sqrt{{a^2}b+a{b^2}}}}$（其中ab=9）．分析 先将题目中的式子化简，然后将ab=9代入即可解答本题．
解答 解：$\frac{\sqrt{a+b}}{\sqrt{{a}^{2}b+a{b}^{2}}}$
=$\frac{\sqrt{a+b}}{\sqrt{ab（a+b）}}$
=$\frac{1}{\sqrt{ab}}$
当ab=9时，原式=$\frac{1}{\sqrt{9}}$=$\frac{1}{3}$．
点评 本题考查二次根式的化简求值，解题的关键是明确如何化简二次根式．
练习册系列答案
小学期末标准试卷系列答案
相关题目
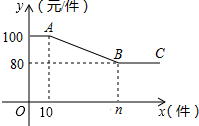小颖妈妈的网店加盟了“小神龙”童装销售，有一款童装的进价为60元/件，售价为100元/件，因为刚加盟，为了增加销量，准备对大客户制定如下“促销优惠”方案：
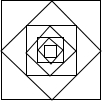如图，以边长为1的正方形的四边中点为顶点作四边形，再以所得四边形四边中点为顶点作四边形，…依次作下去，图中所作的第n个四边形的周长为$4{（\frac{{\sqrt{2}}}{2}）^n}$．
16．在平面直角坐标系中，已知点A（4，2），B（1，3），以原点O为位似中心，相似比为$\frac{1}{2}$，把△ABO缩小，则点A的对应点A′的坐标是（ ）
| A． | （2，1） | B． | （8，4） | C． | （8，4）或（-8，-4） | D． | （2，1）或（-2，-1） |
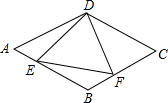如图，在菱形ABCD中，AB=6，∠A=60°，点E、F分别在AB，BC上，且AE=BF，下列结论中：