题目内容
19.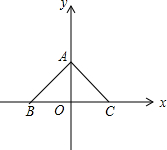 如图,在直角坐标平面内有两点A(0,2)、B(-2,0)、C(2,0).
如图,在直角坐标平面内有两点A(0,2)、B(-2,0)、C(2,0).(1)△ABC的形状是 等腰直角三角形;
(2)求△ABC的面积及AB的长;
(3)在y轴上找一点P,如果△PAB是等腰三角形,请直接写出点P的坐标.
分析 (1)根据点的坐标判断出OA=OB=OC,从而得出结论;
(2)根据点的坐标求出求出BC,OA,再用三角形面积公式即可;
(3)设出点P坐标,根据平面坐标系中,两点间的距离公式表示出BP,AP,再分三种情况计算即可.
解答 解:∵A(0,2)、B(-2,0)、C(2,0).
∴OB=OC=OA,
∴△ABC是等腰三角形,
∵AO⊥BC,
∴△ABC是等腰直角三角形.
故答案为等腰直角三角形,
(2)∵A(0,2)、B(-2,0)、C(2,0).
∴BC=4,OA=2,
∴S△ABC=$\frac{1}{2}$BC×AO=$\frac{1}{2}$×4×2=4,
∵A(0,2)、B(-2,0),
∴AB=$\sqrt{4+4}$=2$\sqrt{2}$,
(3)设点P(0,m),
∵A(0,2)、B(-2,0),
∴AB=2$\sqrt{2}$,BP=$\sqrt{4+{m}^{2}}$,AP=|m-2|,
∵△PAB是等腰三角形,
∴①当AB=BP时,
∴2$\sqrt{2}$=$\sqrt{4+{m}^{2}}$,
∴m=2(舍)或m=-2,
∴P(0,-2),
②当AB=AP时,
∴2$\sqrt{2}$=|m-2|,
∴m=2+2$\sqrt{2}$或m=2-2$\sqrt{2}$,
∴P(0,2-2$\sqrt{2}$)或P(0,2+2$\sqrt{2}$)
③当AP=BP时,
∴|m-2|=$\sqrt{4+{m}^{2}}$,
∴m=0,
∴P(0,0),
∴P(0,-2)或P(0,2-2$\sqrt{2}$)或P(0,2+2$\sqrt{2}$)或P(0,0).
点评 此题是等腰三角形性质,主要考查了等腰三角形的判定,两点间的距离公式,方程的解法,解本题的关键是分类讨论计算即可.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
10.下列各式中,计算正确的是( )
| A. | a3-a2=a | B. | a2+a3=a5 | C. | a8÷a2=a4 | D. | a•a2=a3 |
7.下列运算正确的是( )
| A. | x2+x2=x4 | B. | (-a2)3=-a6 | C. | (a-b)2=a2-b2 | D. | 3a2•2a3=6a6 |
14.某市5月上旬的最高气温如下(单位:℃):28、29、31、29、33,对这组数据,下列说法错误的是( )
| A. | 中位数是31 | B. | 众数是29 | C. | 平均数是30 | D. | 极差是5 |
4.计算$\frac{2x+y}{x-y}$-$\frac{x+2y}{x-y}$的结果是( )
| A. | 1 | B. | $\frac{x+3y}{x-y}$ | C. | x-y | D. | x+3y |
11. 如图是一个几何体的俯视图,则该几何体可能是( )
如图是一个几何体的俯视图,则该几何体可能是( )
 如图是一个几何体的俯视图,则该几何体可能是( )
如图是一个几何体的俯视图,则该几何体可能是( )| A. |  | B. |  | C. |  | D. |  |