题目内容
10．计算：$16×{4^{-1}}+\sqrt{18}÷\sqrt{2}-{（\sqrt{5}-5）^0}-|{-2}|$．分析 根据零指数幂运算、绝对值，二次根式化简进行计算即可．
解答 解：原式=16×$\frac{1}{4}$+3$\sqrt{2}$÷$\sqrt{2}$-1-2
=4+3-1-2
=4．
点评 本题考查了二次根式的混合运算，以及零指数幂运算、绝对值，掌握把二次根式化为最简二次根式是解题的关键．
练习册系列答案
相关题目
18．
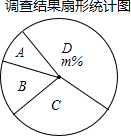2016年3月8日，国务院批复同意自2016年起，将每年4月24日作为“中国航天日”，某市针对中学生开展了航天知识普及活动，活动结束后进行了一次航天知识问卷调查，随机抽取了部分同学的成绩（x均为整数，总分100分），绘制了如下尚不完整的统计图表．
调查结果统计表
根据以上信息解答下列问题：
（1）统计表中，a=450，b=1000，c=0.3；
（2）扇形统计图中，m的值为45，“B”所对应的圆心角的度数是54°；
（3）若参加本次航天知识问卷调查的同学共有20000人，请你估计成绩在95分及以上的学生大约有多少人？
2016年3月8日，国务院批复同意自2016年起，将每年4月24日作为“中国航天日”，某市针对中学生开展了航天知识普及活动，活动结束后进行了一次航天知识问卷调查，随机抽取了部分同学的成绩（x均为整数，总分100分），绘制了如下尚不完整的统计图表．调查结果统计表
| 组别 | 成绩分组（单位：分） | 频数 | 频率 |
| A | 80≤x＜85 | 100 | 0.1 |
| B | 85≤x＜90 | 150 | |
| C | 90≤x＜95 | 300 | c |
| D | 95≤x≤100 | a | |
| 合计 | b | 1 |
（1）统计表中，a=450，b=1000，c=0.3；
（2）扇形统计图中，m的值为45，“B”所对应的圆心角的度数是54°；
（3）若参加本次航天知识问卷调查的同学共有20000人，请你估计成绩在95分及以上的学生大约有多少人？
尺规作图：已知△ABC，如图．
15．
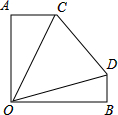如图，A在O的正北方向，B在O的正东方向，且OA=OB．某一时刻，甲车从A出发，以60km/h的速度朝正东方向行驶，与此同时，乙车从B出发，以40km/h的速度朝正北方向行驶．1小时后，位于点O处的观察员发现甲、乙两车之间的夹角为45°，即∠COD=45°，此时，甲、乙两人相距的距离为（ ）
如图，A在O的正北方向，B在O的正东方向，且OA=OB．某一时刻，甲车从A出发，以60km/h的速度朝正东方向行驶，与此同时，乙车从B出发，以40km/h的速度朝正北方向行驶．1小时后，位于点O处的观察员发现甲、乙两车之间的夹角为45°，即∠COD=45°，此时，甲、乙两人相距的距离为（ ）| A． | 90km | B． | 50$\sqrt{2}$km | C． | 20$\sqrt{13}$km | D． | 100km |
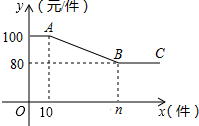小颖妈妈的网店加盟了“小神龙”童装销售，有一款童装的进价为60元/件，售价为100元/件，因为刚加盟，为了增加销量，准备对大客户制定如下“促销优惠”方案：