题目内容
4.不等式组$\left\{\begin{array}{l}{3(x+1)>x-1}\\{-\frac{2}{3}x+3≥2}\end{array}\right.$的整数解的和是( )| A. | -1 | B. | 1 | C. | 0 | D. | 1 |
分析 先解出不等式组的解集,从而可以得到不等式组的整数解,从而可以得到不等式组$\left\{\begin{array}{l}{3(x+1)>x-1}\\{-\frac{2}{3}x+3≥2}\end{array}\right.$的整数解的和.
解答 解:$\left\{\begin{array}{l}{3(x+1)>x-1}\\{-\frac{2}{3}x+3≥2}\end{array}\right.$
解得,-2<x≤$\frac{3}{2}$,
∴$\left\{\begin{array}{l}{3(x+1)>x-1}\\{-\frac{2}{3}x+3≥2}\end{array}\right.$的整数解是x=-1,x=0,x=1,
∵(-1)+0+1=0,
故$\left\{\begin{array}{l}{3(x+1)>x-1}\\{-\frac{2}{3}x+3≥2}\end{array}\right.$的整数解得和是0,
故选C.
点评 本题考查一元一次不等式组的整数解,解题的关键是明确解一元一次不等式组的方法.

练习册系列答案
相关题目
14.某市5月上旬的最高气温如下(单位:℃):28、29、31、29、33,对这组数据,下列说法错误的是( )
| A. | 中位数是31 | B. | 众数是29 | C. | 平均数是30 | D. | 极差是5 |
15.钓鱼岛是中国的固有领土,其渔业资源十分丰富,年捕鱼量达15万吨.数据15万用科学记数法表示为( )
| A. | 1.5×104 | B. | 1.5×105 | C. | 15×104 | D. | 15×105 |
8.如果四边形内的一个点到四条边的距离相等,那么这个四边形一定有( )
| A. | 一组邻边相等 | B. | 一组对边平行 | ||
| C. | 两组对边分别相等 | D. | 两组对边的和相等 |
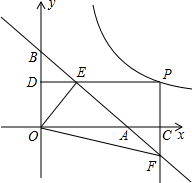 如图,已知直线y=-x+1与x轴交于A点,与y轴交于B点,P(a,b)为双曲线y=$\frac{1}{2x}$(x>0)上一动点,过P点分别作x轴、y轴的垂线,垂足分别为C、D,交直线AB于点E、F
如图,已知直线y=-x+1与x轴交于A点,与y轴交于B点,P(a,b)为双曲线y=$\frac{1}{2x}$(x>0)上一动点,过P点分别作x轴、y轴的垂线,垂足分别为C、D,交直线AB于点E、F 尺规作图:已知△ABC,如图.
尺规作图:已知△ABC,如图.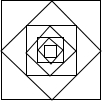 如图,以边长为1的正方形的四边中点为顶点作四边形,再以所得四边形四边中点为顶点作四边形,…依次作下去,图中所作的第n个四边形的周长为$4{(\frac{{\sqrt{2}}}{2})^n}$.
如图,以边长为1的正方形的四边中点为顶点作四边形,再以所得四边形四边中点为顶点作四边形,…依次作下去,图中所作的第n个四边形的周长为$4{(\frac{{\sqrt{2}}}{2})^n}$.