题目内容
18.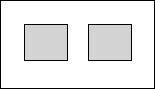 某广场绿化工程中有一块长2千米,宽1千米的矩形空地,计划在其中修建两块相同的矩形绿地,两块绿地之间既周边留有宽度相等的人行通道(如图),并在这些人行通道铺上瓷砖,要求铺瓷砖的面积是矩形空地面积的$\frac{1}{2}$,设人行通道的宽度为x千米,则下列方程正确的是( )
某广场绿化工程中有一块长2千米,宽1千米的矩形空地,计划在其中修建两块相同的矩形绿地,两块绿地之间既周边留有宽度相等的人行通道(如图),并在这些人行通道铺上瓷砖,要求铺瓷砖的面积是矩形空地面积的$\frac{1}{2}$,设人行通道的宽度为x千米,则下列方程正确的是( )| A. | (2-3x)(1-2x)=1 | B. | $\frac{1}{2}$(2-3x)(1-2x)=1 | C. | $\frac{1}{4}$(2-3x)(1-2x)=1 | D. | $\frac{1}{4}$(2-3x)(1-2x)=2 |
分析 根据题意分别表示出矩形绿地的长和宽,再由铺瓷砖的面积是矩形空地面积的$\frac{1}{2}$,即矩形绿地的面积=$\frac{1}{2}$矩形空地面积,可列方程.
解答 解:设人行通道的宽度为x千米,
则矩形绿地的长为:$\frac{1}{2}$(2-3x),宽为(1-2x),
由题意可列方程:2×$\frac{1}{2}$(2-3x)(1-2x)=$\frac{1}{2}$×2×1,
即:(2-3x)(1-2x)=1,
故选:A.
点评 本题主要考查根据实际问题列方程的能力,分析题意准确抓住相等关系是解方程的关键.

练习册系列答案
相关题目
13.某地区2015年的交于投入为2.2亿元,计划在未来两年终总共再投入5亿元,设每年教育投入的平均增长率为x,根据题意,可列方程为( )
| A. | 2.2(1+2x)2=5 | B. | 2.2(1+2x)3=5 | ||
| C. | 2.2(1+x)+2.2(1+x2)=5 | D. | 2.2(1+x)+2.2(1+x)3=5 |
8.下列各组数据中的是三个数作为三角形的边长,其中能构成直角三角形的是( )
| A. | 1,$\sqrt{2}$,$\sqrt{3}$ | B. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$ | C. | 5,6,7 | D. | 7,8,9 |
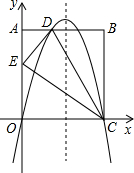 如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系,抛物线y=ax2+bx+c经过O,D,C三点.
如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系,抛物线y=ax2+bx+c经过O,D,C三点.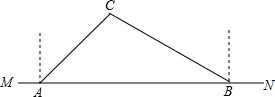 如图,要在后羿公园内的东西方向的两地之间修一条游客步行道路MN,已知C点周围50米范围内为中共华工委纪念馆,在MN上的点A处测得C在A的北偏东45°方向上,从A向东走150米到达B处,测得C在点B的北偏西60°方向上.
如图,要在后羿公园内的东西方向的两地之间修一条游客步行道路MN,已知C点周围50米范围内为中共华工委纪念馆,在MN上的点A处测得C在A的北偏东45°方向上,从A向东走150米到达B处,测得C在点B的北偏西60°方向上.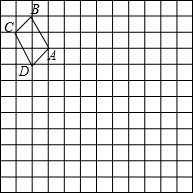 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点四边形ABCD(顶点是网格线的交点),按要求画出四边形AB1C1D1和四边形AB2C2D2.
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点四边形ABCD(顶点是网格线的交点),按要求画出四边形AB1C1D1和四边形AB2C2D2.