题目内容
9.点A(x1,y1),B(x2,y2)是反比例函数y=-$\frac{2}{x}$图象上的两点,若x1>x2>0,则y1>y2(填“>”“<”“=”).分析 先根据反比例函数的解析式判断出函数图象所在的象限,再根据x1>x2>0即可得出结论.
解答 解:∵反比例函数y=-$\frac{2}{x}$中,k=-2<0,
∴函数图象的两个分支分别位于二四象限,且在每一象限内,y随x的增大而增大,
∵x1>x2>0,
∴y1>y2.
故答案为:>.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数的图象与系数的关系是解答此题的关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
4.计算x2•x3÷x的结果是( )
| A. | x4 | B. | x5 | C. | x6 | D. | x7 |
18.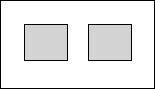 某广场绿化工程中有一块长2千米,宽1千米的矩形空地,计划在其中修建两块相同的矩形绿地,两块绿地之间既周边留有宽度相等的人行通道(如图),并在这些人行通道铺上瓷砖,要求铺瓷砖的面积是矩形空地面积的$\frac{1}{2}$,设人行通道的宽度为x千米,则下列方程正确的是( )
某广场绿化工程中有一块长2千米,宽1千米的矩形空地,计划在其中修建两块相同的矩形绿地,两块绿地之间既周边留有宽度相等的人行通道(如图),并在这些人行通道铺上瓷砖,要求铺瓷砖的面积是矩形空地面积的$\frac{1}{2}$,设人行通道的宽度为x千米,则下列方程正确的是( )
 某广场绿化工程中有一块长2千米,宽1千米的矩形空地,计划在其中修建两块相同的矩形绿地,两块绿地之间既周边留有宽度相等的人行通道(如图),并在这些人行通道铺上瓷砖,要求铺瓷砖的面积是矩形空地面积的$\frac{1}{2}$,设人行通道的宽度为x千米,则下列方程正确的是( )
某广场绿化工程中有一块长2千米,宽1千米的矩形空地,计划在其中修建两块相同的矩形绿地,两块绿地之间既周边留有宽度相等的人行通道(如图),并在这些人行通道铺上瓷砖,要求铺瓷砖的面积是矩形空地面积的$\frac{1}{2}$,设人行通道的宽度为x千米,则下列方程正确的是( )| A. | (2-3x)(1-2x)=1 | B. | $\frac{1}{2}$(2-3x)(1-2x)=1 | C. | $\frac{1}{4}$(2-3x)(1-2x)=1 | D. | $\frac{1}{4}$(2-3x)(1-2x)=2 |
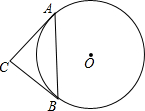 如图,已知⊙O的半径是4cm,弦AB=4$\sqrt{2}$cm,AC是⊙O的切线,切AC=4cm,连接BC.
如图,已知⊙O的半径是4cm,弦AB=4$\sqrt{2}$cm,AC是⊙O的切线,切AC=4cm,连接BC. 如图,直线a∥b,直线c分别与a,b相交,∠1=45°,则∠2的度数为135°.
如图,直线a∥b,直线c分别与a,b相交,∠1=45°,则∠2的度数为135°.