题目内容
8．下列各组数据中的是三个数作为三角形的边长，其中能构成直角三角形的是（ ）| A． | 1，$\sqrt{2}$，$\sqrt{3}$ | B． | $\sqrt{3}$，$\sqrt{4}$，$\sqrt{5}$ | C． | 5，6，7 | D． | 7，8，9 |
分析 知道三条边的大小，用较小的两条边的平方和与最大的边的平方比较，如果相等，则三角形为直角三角形；否则不是．
解答 解：A、∵12+（$\sqrt{2}$）2=（$\sqrt{3}$）2，∴能构成直角三角形；
B、（$\sqrt{3}$）2+（$\sqrt{4}$）2≠（$\sqrt{5}$）2，∴不能构成直角三角形；
C、52+62≠72，∴不能构成直角三角形；
D、∵72+82≠92，∴不能构成直角三角形．
故选A．
点评 本题考查的是用勾股定理的逆定理判断三角形的形状，即若三角形的三边符合a2+b2=c2，则此三角形是直角三角形．
练习册系列答案
相关题目
18．
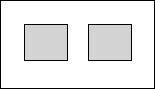某广场绿化工程中有一块长2千米，宽1千米的矩形空地，计划在其中修建两块相同的矩形绿地，两块绿地之间既周边留有宽度相等的人行通道（如图），并在这些人行通道铺上瓷砖，要求铺瓷砖的面积是矩形空地面积的$\frac{1}{2}$，设人行通道的宽度为x千米，则下列方程正确的是（ ）
某广场绿化工程中有一块长2千米，宽1千米的矩形空地，计划在其中修建两块相同的矩形绿地，两块绿地之间既周边留有宽度相等的人行通道（如图），并在这些人行通道铺上瓷砖，要求铺瓷砖的面积是矩形空地面积的$\frac{1}{2}$，设人行通道的宽度为x千米，则下列方程正确的是（ ）| A． | （2-3x）（1-2x）=1 | B． | $\frac{1}{2}$（2-3x）（1-2x）=1 | C． | $\frac{1}{4}$（2-3x）（1-2x）=1 | D． | $\frac{1}{4}$（2-3x）（1-2x）=2 |
3．
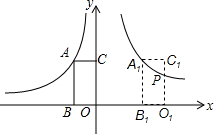如图，在平面直角坐标系中，矩形ABOC的两边在坐标轴上，OB=2，点A在函数y=-$\frac{8}{x}$（x＜0）的图象上．将矩形向右平移6个单位长度到A1B1O1C1的位置，此时点A1在函数y=$\frac{k}{x}$（x＞0）的图象上，边C1O1与此图象交于点P，则点P的纵坐标为（ ）
如图，在平面直角坐标系中，矩形ABOC的两边在坐标轴上，OB=2，点A在函数y=-$\frac{8}{x}$（x＜0）的图象上．将矩形向右平移6个单位长度到A1B1O1C1的位置，此时点A1在函数y=$\frac{k}{x}$（x＞0）的图象上，边C1O1与此图象交于点P，则点P的纵坐标为（ ）| A． | $\frac{3}{4}$ | B． | $\frac{5}{3}$ | C． | $\frac{5}{2}$ | D． | $\frac{8}{3}$ |
20．下列图形中，既是轴对称图形，又是中心对称图形的是（ ）
| A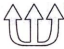． |  | B． |  | C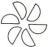． |  | D． |  |
17．先化简，再求值（$\frac{{x}^{2}-4}{{x}^{2}-4x+4}$+$\frac{2-x}{x+2}$）÷$\frac{x}{x-2}$（其中x=3），其计算结果是（ ）
| A． | -$\frac{8}{5}$ | B． | 8 | C． | -8 | D． | $\frac{8}{5}$ |