题目内容
3.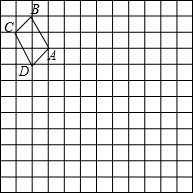 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点四边形ABCD(顶点是网格线的交点),按要求画出四边形AB1C1D1和四边形AB2C2D2.
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点四边形ABCD(顶点是网格线的交点),按要求画出四边形AB1C1D1和四边形AB2C2D2.(1)以A为旋转中心,将四边形ABCD顺时针旋转90°,得到四边形AB1C1D1;
(2)以A为位似中心,将四边形ABCD作位似变换,且放大到原来的两倍,得到四边形AB2C2D2.
分析 (1)利用网格特点和旋转的性质画出点B、C、D的对应点B1、C1、D1即可得到四边形AB1C1D1;
(2)延长BA到B2,使B2A=2BA,则点B2为点B的对应点,同样方法作出点C和D的对应点C2、D2,则四边形AB2C2D2满足条件.
解答 解:(1)如图,四边形AB1C1D1为所作;
(2)如图,四边形AB2C2D2为所作.
点评 本题考查了作图-位似变换:画位似图形的一般步骤为,先确定位似中心;再分别连接并延长位似中心和能代表原图的关键点;接着根据位似比,确定能代表所作的位似图形的关键点;然后顺次连接上述各点,得到放大或缩小的图形.也考查了旋转变换.

练习册系列答案
相关题目
11.若x1,x2是一元二次方程x2+4x-2016=0的两个根,则x1+x2-x1x2的值是( )
| A. | -2012 | B. | -2020 | C. | 2012 | D. | 2020 |
18.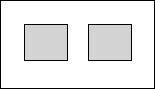 某广场绿化工程中有一块长2千米,宽1千米的矩形空地,计划在其中修建两块相同的矩形绿地,两块绿地之间既周边留有宽度相等的人行通道(如图),并在这些人行通道铺上瓷砖,要求铺瓷砖的面积是矩形空地面积的$\frac{1}{2}$,设人行通道的宽度为x千米,则下列方程正确的是( )
某广场绿化工程中有一块长2千米,宽1千米的矩形空地,计划在其中修建两块相同的矩形绿地,两块绿地之间既周边留有宽度相等的人行通道(如图),并在这些人行通道铺上瓷砖,要求铺瓷砖的面积是矩形空地面积的$\frac{1}{2}$,设人行通道的宽度为x千米,则下列方程正确的是( )
 某广场绿化工程中有一块长2千米,宽1千米的矩形空地,计划在其中修建两块相同的矩形绿地,两块绿地之间既周边留有宽度相等的人行通道(如图),并在这些人行通道铺上瓷砖,要求铺瓷砖的面积是矩形空地面积的$\frac{1}{2}$,设人行通道的宽度为x千米,则下列方程正确的是( )
某广场绿化工程中有一块长2千米,宽1千米的矩形空地,计划在其中修建两块相同的矩形绿地,两块绿地之间既周边留有宽度相等的人行通道(如图),并在这些人行通道铺上瓷砖,要求铺瓷砖的面积是矩形空地面积的$\frac{1}{2}$,设人行通道的宽度为x千米,则下列方程正确的是( )| A. | (2-3x)(1-2x)=1 | B. | $\frac{1}{2}$(2-3x)(1-2x)=1 | C. | $\frac{1}{4}$(2-3x)(1-2x)=1 | D. | $\frac{1}{4}$(2-3x)(1-2x)=2 |
15.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
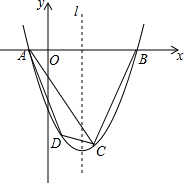 如图,已知二次函数的图象M经过A(-1,0),B(4,0),C(2,-6)三点.
如图,已知二次函数的图象M经过A(-1,0),B(4,0),C(2,-6)三点.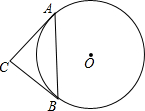 如图,已知⊙O的半径是4cm,弦AB=4$\sqrt{2}$cm,AC是⊙O的切线,切AC=4cm,连接BC.
如图,已知⊙O的半径是4cm,弦AB=4$\sqrt{2}$cm,AC是⊙O的切线,切AC=4cm,连接BC.