题目内容
 如图,AB是⊙O的直径,AM,BN分别切⊙O于点A,B,CD交AM,BN于点D,C,DO平分∠ADC.
如图,AB是⊙O的直径,AM,BN分别切⊙O于点A,B,CD交AM,BN于点D,C,DO平分∠ADC.(1)求证:CD是⊙O的切线;
(2)若AD=4,BC=9,求OD的长.
考点:切线的判定,相似三角形的判定与性质
专题:证明题
分析:(1)过O点作OE⊥CD于点E,根据切线的性质由AM切⊙O于点A得OA⊥AD,再根据角平分线定理得到OE=OA,然后根据切线的判定定理得到CD是⊙O的切线;
(2)过D作DF⊥BC于F,根据切线的性质得到AB⊥AD,AB⊥BC,则得到四边形ABFD为矩形,得到BF=AD=4,所以CF=BC-BF=5,再利用切线长定理得DA=DE=4,CE=CB=9,所以DC=AD+BC=13,在Rt△DCF中,利用勾股定理计算出DF=12,则AB=12,所以OA=6,然后在Rt△OAD中,利用勾股定理可计算出OD.
(2)过D作DF⊥BC于F,根据切线的性质得到AB⊥AD,AB⊥BC,则得到四边形ABFD为矩形,得到BF=AD=4,所以CF=BC-BF=5,再利用切线长定理得DA=DE=4,CE=CB=9,所以DC=AD+BC=13,在Rt△DCF中,利用勾股定理计算出DF=12,则AB=12,所以OA=6,然后在Rt△OAD中,利用勾股定理可计算出OD.
解答: (1)证明:过O点作OE⊥CD于点E,如图,
(1)证明:过O点作OE⊥CD于点E,如图,
∵AM切⊙O于点A,
∴OA⊥AD,
∵DO平分∠ADC,
∴OE=OA,
∵OA为⊙O的半径,
∴OE是⊙O的半径,且OE⊥DC,
∴CD是⊙O的切线;
(2)解:过D作DF⊥BC于F,如图,
∵AB是⊙O的直径,AM,BN分别切⊙O于点A,B,
∴AB⊥AD,AB⊥BC,
∴四边形ABFD为矩形,
∴BF=AD=4,
∴CF=BC-BF=5,
∵DC、AM、BC为圆的切线,
∴DA=DE=4,CE=CB=9,
∴DC=AD+BC=13,
在Rt△DCF中,DF=
=12,
∴AB=12,
∴OA=6,
在Rt△OAD中,OD=
=
=2
.
 (1)证明:过O点作OE⊥CD于点E,如图,
(1)证明:过O点作OE⊥CD于点E,如图,∵AM切⊙O于点A,
∴OA⊥AD,
∵DO平分∠ADC,
∴OE=OA,
∵OA为⊙O的半径,
∴OE是⊙O的半径,且OE⊥DC,
∴CD是⊙O的切线;
(2)解:过D作DF⊥BC于F,如图,
∵AB是⊙O的直径,AM,BN分别切⊙O于点A,B,
∴AB⊥AD,AB⊥BC,
∴四边形ABFD为矩形,
∴BF=AD=4,
∴CF=BC-BF=5,
∵DC、AM、BC为圆的切线,
∴DA=DE=4,CE=CB=9,
∴DC=AD+BC=13,
在Rt△DCF中,DF=
| DC2-DF2 |
∴AB=12,
∴OA=6,
在Rt△OAD中,OD=
| OA2+AD2 |
| 62+42 |
| 13 |
点评:本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了切线的性质、切线长定理、勾股定理.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
下列运算正确的是( )
| A、3x2-x2=3 |
| B、x2•x4=x6 |
| C、x6÷x3=x2 |
| D、2(x2)3=6x6 |
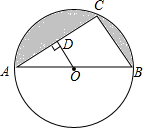 如图,已知AB是⊙O的直径,点C在⊙O上,且AB=13,BC=5.
如图,已知AB是⊙O的直径,点C在⊙O上,且AB=13,BC=5. 如图,在矩形ABCD中,AB=4,BC=3,点O为对角线BD的中点,点P从点A出发,沿折线AD-DO-OC以每秒1个单位长度的速度向终点C运动,当点P与点A不重合时,过点P作PQ⊥AB于点Q,以PQ为边向右作正方形PQMN,设正方形PQMN与△ABD重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).
如图,在矩形ABCD中,AB=4,BC=3,点O为对角线BD的中点,点P从点A出发,沿折线AD-DO-OC以每秒1个单位长度的速度向终点C运动,当点P与点A不重合时,过点P作PQ⊥AB于点Q,以PQ为边向右作正方形PQMN,设正方形PQMN与△ABD重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒). 学校为丰富学生课间自由活动的内容,随机选取本校部分学生进行调查,调查内容是“你最喜欢的自由活动项目是什么?”,已知喜欢“跳绳”的学生占被调查人数的20%,整理收集到的数据后,绘制成如图.
学校为丰富学生课间自由活动的内容,随机选取本校部分学生进行调查,调查内容是“你最喜欢的自由活动项目是什么?”,已知喜欢“跳绳”的学生占被调查人数的20%,整理收集到的数据后,绘制成如图.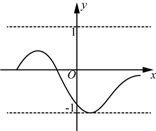 对某一个函数给出如下定义:若存在实数M>0,对于任意的函数值y,都满足-M≤y≤M,则称这个函数是有界函数,在所有满足条件的M中,其最小值称为这个函数的边界值.例如,如图中的函数是有界函数,其边界值是1.
对某一个函数给出如下定义:若存在实数M>0,对于任意的函数值y,都满足-M≤y≤M,则称这个函数是有界函数,在所有满足条件的M中,其最小值称为这个函数的边界值.例如,如图中的函数是有界函数,其边界值是1.