题目内容
甲、乙两名射击运动员在某场测试中各射击20次,测试成绩如表:
则 (选填甲、乙)运动员测试成绩更稳定.
| 乙的成绩 | ||||
| 环数 | 7 | 8 | 9 | 10 |
| 频数 | 6 | 4 | 4 | 6 |
| 甲的成绩 | ||||
| 环数 | 7 | 8 | 9 | 10 |
| 频数 | 4 | 6 | 6 | 4 |
考点:方差
专题:
分析:分别做出甲的平均成绩和乙的平均成绩,两个人的平均成绩相等,再利用方差公式分别算出甲、乙两位运动员的方差,可知S2甲<S2乙,所以甲运动员测试成绩更稳定.
解答:解:甲的平均成绩是
=8.5,
乙的平均成绩是
=8.5,
甲的方差是S2甲=2.25×0.2+0.25×0.3+0.25×0.3+2.25×0.2=1.05,
乙的方差是S2乙=2.25×0.3+0.25×0.2+0.25×0.2+2.25×0.3=1.225,
∵S2甲<S2乙,
∴运动员测试成绩更稳定的是甲;
故答案为:甲.
| 7×4+8×6+9×6+10×4 |
| 20 |
乙的平均成绩是
| 7×6+8×4+9×4+10×6 |
| 20 |
甲的方差是S2甲=2.25×0.2+0.25×0.3+0.25×0.3+2.25×0.2=1.05,
乙的方差是S2乙=2.25×0.3+0.25×0.2+0.25×0.2+2.25×0.3=1.225,
∵S2甲<S2乙,
∴运动员测试成绩更稳定的是甲;
故答案为:甲.
点评:本题考查一组数据的平均数和方差,一般地设n个数据,x1,x2,…xn的平均数为
,则方差S2=
[(x1-
)2+(x2-
)2+…+(xn-
)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
. |
| x |
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |

练习册系列答案
相关题目
下列计算正确的是( )
| A、2a+b=2ab |
| B、a3÷a=a2 |
| C、(a-1)2=a2-1 |
| D、(2a)3=6a3 |
 如图,AB是⊙O的直径,AM,BN分别切⊙O于点A,B,CD交AM,BN于点D,C,DO平分∠ADC.
如图,AB是⊙O的直径,AM,BN分别切⊙O于点A,B,CD交AM,BN于点D,C,DO平分∠ADC.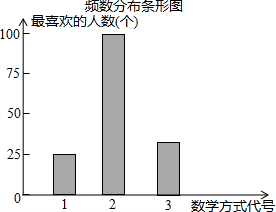 某中学为促进课堂教学,提高教学质量,对七年级学生进行了一次“你最喜欢的课堂教学方式”的问卷调查.根据收回的问卷,学校绘制了“频数分布表”和“频数分布条形图”.请你根据图表中提供的信息,解答下列问题.
某中学为促进课堂教学,提高教学质量,对七年级学生进行了一次“你最喜欢的课堂教学方式”的问卷调查.根据收回的问卷,学校绘制了“频数分布表”和“频数分布条形图”.请你根据图表中提供的信息,解答下列问题. 如图,四边形ABCD是等腰梯形,若其四边满足长度的众数为5,平均数为
如图,四边形ABCD是等腰梯形,若其四边满足长度的众数为5,平均数为 如图,已知在矩形ABCD中,AB=2,BC=3,M是边BC的中点,则点D到AM的距离DE等于
如图,已知在矩形ABCD中,AB=2,BC=3,M是边BC的中点,则点D到AM的距离DE等于 如图,当太阳在A处时,小明测得某树的影长为2米,当太阳在B处时又测得该树的影长为8米.若两次日照的光线互相垂直,则这颗树的高度为
如图,当太阳在A处时,小明测得某树的影长为2米,当太阳在B处时又测得该树的影长为8米.若两次日照的光线互相垂直,则这颗树的高度为 如图,一次函数y=-x+m的图象和y轴交于点B,与正比例函数y=
如图,一次函数y=-x+m的图象和y轴交于点B,与正比例函数y=