��Ŀ����
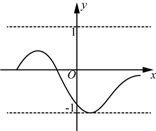 ��ijһ�������������¶��壺������ʵ��M��0����������ĺ���ֵy��������-M��y��M���������������н纯��������������������M�У�����Сֵ��Ϊ��������ı߽�ֵ�����磬��ͼ�еĺ������н纯������߽�ֵ��1��
��ijһ�������������¶��壺������ʵ��M��0����������ĺ���ֵy��������-M��y��M���������������н纯��������������������M�У�����Сֵ��Ϊ��������ı߽�ֵ�����磬��ͼ�еĺ������н纯������߽�ֵ��1����1���ֱ��жϺ��� y=
| 1 |
| x |
��2��������y=-x+1��a��x��b��b��a���ı߽�ֵ��2����������������ֵҲ��2����b��ȡֵ��Χ��
��3�������� y=x2��-1��x��m��m��0����ͼ������ƽ��m����λ���õ��ĺ����ı߽�ֵ��t����m��ʲô��Χʱ������
| 3 |
| 4 |
���㣺���κ����ۺ���
ר�⣺�����ۺ���,ѹ����
��������1�������н纯���Ķ���ͺ����ı߽�ֵ�Ķ�����д��⣻
��2�����ݺ����������ԡ��߽�ֵȷ��a=-1��Ȼ���ɡ����������ֵҲ��2������b��ȡֵ��Χ��
��3����Ҫ�������ۣ�m��1��m��1����������ɺ�������ʽ�õ��ú���ͼ����㣨-1��1������0��0��������ƽ�Ƶ����ʵõ�������ƽ�ƺ������ֱ��ǣ�-1��1-m������0��-m��������ɺ����߽�ֵ�Ķ����г�����ʽ
��1-m��1��-1��-m��-
������mȡֵ��Χ��0��m��
��
��m��1��
��2�����ݺ����������ԡ��߽�ֵȷ��a=-1��Ȼ���ɡ����������ֵҲ��2������b��ȡֵ��Χ��
��3����Ҫ�������ۣ�m��1��m��1����������ɺ�������ʽ�õ��ú���ͼ����㣨-1��1������0��0��������ƽ�Ƶ����ʵõ�������ƽ�ƺ������ֱ��ǣ�-1��1-m������0��-m��������ɺ����߽�ֵ�Ķ����г�����ʽ
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
����⣺��1�������н纯���Ķ���֪������y=
��x��0�������н纯����
y=x+1��-4��x��2�����н纯�����߽�ֵΪ��2+1=3��
��2���ߺ���y=-x+1��ͼ����y��x���������С��
�൱x=aʱ��y=-a+1=2����a=-1
��x=bʱ��y=-b+1����
��
��-1��b��3��
��3����m��1����������ƽ��m����λ��x=0ʱ������ֵС��-1����ʱ�����ı߽�t��1�������ⲻ������m��1��
��x=-1ʱ��y=1 �����㣨-1��1��
��x=0ʱ��y��С=0�������㣨0��0����
������ƽ��m����λ����
��-1��1-m������0��-m��
��1-m��1��-1��-m��-
��
��0��m��
��
��m��1��
| 1 |
| x |
y=x+1��-4��x��2�����н纯�����߽�ֵΪ��2+1=3��
��2���ߺ���y=-x+1��ͼ����y��x���������С��
�൱x=aʱ��y=-a+1=2����a=-1
��x=bʱ��y=-b+1����
|
��-1��b��3��
��3����m��1����������ƽ��m����λ��x=0ʱ������ֵС��-1����ʱ�����ı߽�t��1�������ⲻ������m��1��
��x=-1ʱ��y=1 �����㣨-1��1��
��x=0ʱ��y��С=0�������㣨0��0����
������ƽ��m����λ����
��-1��1-m������0��-m��
| 3 |
| 4 |
| 3 |
| 4 |
��0��m��
| 1 |
| 4 |
| 3 |
| 4 |
���������⿼���˶��κ����ۺ����ͣ����ա��н纯�����͡��н纯���ı߽�ֵ���Ķ����ǽ���Ĺؼ���

��ϰ��ϵ�д�
 ѧ�����νӽ̲��Ͼ���ѧ������ϵ�д�
ѧ�����νӽ̲��Ͼ���ѧ������ϵ�д� Сѧ������ҵϵ�д�
Сѧ������ҵϵ�д�
�����Ŀ
���м�����ȷ���ǣ�������
| A��2a+b=2ab |
| B��a3��a=a2 |
| C����a-1��2=a2-1 |
| D����2a��3=6a3 |
 ��ͼ��AB�ǡ�O��ֱ����AM��BN�ֱ��С�O�ڵ�A��B��CD��AM��BN�ڵ�D��C��DOƽ�֡�ADC��
��ͼ��AB�ǡ�O��ֱ����AM��BN�ֱ��С�O�ڵ�A��B��CD��AM��BN�ڵ�D��C��DOƽ�֡�ADC��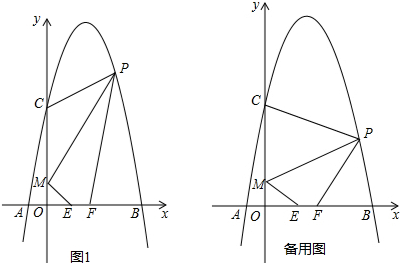
 ��ͼ����A�ǡ�O��һ�㣬OA��AB����OA=1��AB=
��ͼ����A�ǡ�O��һ�㣬OA��AB����OA=1��AB=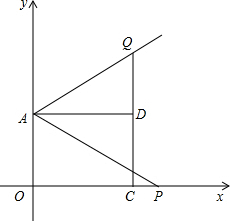 ��ͼ���ھ���AOCD�У�AO=3��0C=4����AO��OC������ֱ��Ϊx�ᣬy�Ὠ��ֱ������ϵ����P��OC�ӳ�����һ�㣬������AP��ֱ��AD���ۣ�������CD�ڵ�Q��
��ͼ���ھ���AOCD�У�AO=3��0C=4����AO��OC������ֱ��Ϊx�ᣬy�Ὠ��ֱ������ϵ����P��OC�ӳ�����һ�㣬������AP��ֱ��AD���ۣ�������CD�ڵ�Q��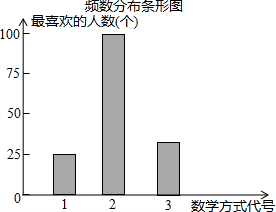 ij��ѧΪ�ٽ����ý�ѧ����߽�ѧ�����������꼶ѧ��������һ�Ρ�����ϲ���Ŀ��ý�ѧ��ʽ�����ʾ����飮�����ջص��ʾ���ѧУ�����ˡ�Ƶ���ֲ������͡�Ƶ���ֲ�����ͼ�����������ͼ�����ṩ����Ϣ������������⣮
ij��ѧΪ�ٽ����ý�ѧ����߽�ѧ�����������꼶ѧ��������һ�Ρ�����ϲ���Ŀ��ý�ѧ��ʽ�����ʾ����飮�����ջص��ʾ���ѧУ�����ˡ�Ƶ���ֲ������͡�Ƶ���ֲ�����ͼ�����������ͼ�����ṩ����Ϣ������������⣮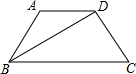 ��ͼ���ı���ABCD�ǵ������Σ������ı����㳤�ȵ�����Ϊ5��ƽ����Ϊ
��ͼ���ı���ABCD�ǵ������Σ������ı����㳤�ȵ�����Ϊ5��ƽ����Ϊ