题目内容
计算[
]的值．其中，2012共出现了2012次，[x]表示不超过实数x的最大整数．
2012+
|
考点：取整计算,算术平方根,不等式的性质
专题：计算题
分析：为了方便起见，设xn=
，其中2012共出现了n次，n为正整数．易得44＜x1＜45，由于x2=
，根据不等式的性质可推出45＜x2＜46；用同样的方法，由45＜x2＜46可以推出45＜x3＜46；以此类推，可以得到；当n≥2时，45＜xn＜46，从而有[xn]=45，故原式=[x2012]=45．
2012+
|
| 2012+x1 |
解答：解：设xn=
，其中2012共出现了n次，n为正整数．
当n=1时，x1=
．
∵44=
＜
＜
=45，
∴44＜x1＜45．
当n=2时，x2=
．
∵44＜x1＜45，
∴45=
＜
＜x2＜
＜
=46．
∴45＜x2＜46．
当n=3时，x3=
．
∵45＜x2＜46，
∴45=
＜
＜x3＜
＜
=46．
∴45＜x3＜46．
∴由45＜x2＜46可以推出45＜x3＜46．
同理可得：
由45＜x3＜46可以推出45＜x4＜46；
由45＜x4＜46可以推出45＜x5＜46；
由45＜x5＜46可以推出45＜x6＜46；
…
由45＜xn-1＜46可以推出45＜xn＜46．（n≥4）
∴当n≥2时，45＜xn＜46，此时[xn]=45．
∴原式=[x2012]=45．
2012+
|
当n=1时，x1=
| 2012 |
∵44=
| 1936 |
| 2012 |
| 2025 |
∴44＜x1＜45．
当n=2时，x2=
| 2012+x1 |
∵44＜x1＜45，
∴45=
| 2025 |
| 2012+44 |
| 2012+45 |
| 2116 |
∴45＜x2＜46．
当n=3时，x3=
| 2012+x2 |
∵45＜x2＜46，
∴45=
| 2025 |
| 2012+45 |
| 2012+46 |
| 2116 |
∴45＜x3＜46．
∴由45＜x2＜46可以推出45＜x3＜46．
同理可得：
由45＜x3＜46可以推出45＜x4＜46；
由45＜x4＜46可以推出45＜x5＜46；
由45＜x5＜46可以推出45＜x6＜46；
…
由45＜xn-1＜46可以推出45＜xn＜46．（n≥4）
∴当n≥2时，45＜xn＜46，此时[xn]=45．
∴原式=[x2012]=45．
点评：本题考查了不等式的性质、算术平方根等知识，并注重对类比、归纳等推理能力的考查，而通过类比、归纳得出“当n≥2时，45＜xn＜46，则[xn]=45”是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
2的相反数是（ ）
| A、2 | ||
| B、-2 | ||
C、-
| ||
D、
|
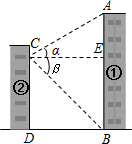某中学九年级学生在学习“直角三角形的边角关系”时，组织开展测量物体高度的实践活动．在活动中，某小组为了测量校园内①号楼AB的高度（如图），站在②号楼的C处，测得①号楼顶部A处的仰角α=30°，底部B处的俯角β=45°，已知两幢楼的水平距离BD为18米，求①号楼AB的高度．（结果保留根号）
如图，AB是⊙O的直径，AM，BN分别切⊙O于点A，B，CD交AM，BN于点D，C，DO平分∠ADC．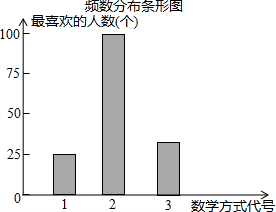
某中学为促进课堂教学，提高教学质量，对七年级学生进行了一次“你最喜欢的课堂教学方式”的问卷调查．根据收回的问卷，学校绘制了“频数分布表”和“频数分布条形图”．请你根据图表中提供的信息，解答下列问题．