题目内容
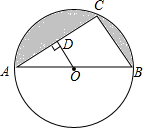 如图,已知AB是⊙O的直径,点C在⊙O上,且AB=13,BC=5.
如图,已知AB是⊙O的直径,点C在⊙O上,且AB=13,BC=5.(1)求sin∠BAC的值.
(2)如果OD⊥AC,垂足为D,求AD的长.
(3)求图中阴影部分的面积(精确到0.1).
考点:垂径定理,三角形中位线定理,扇形面积的计算,解直角三角形
专题:
分析:(1)根据圆周角定理求出∠ACB=90°,解直角三角形即可;
(2)根据勾股定理求出AC,根据垂径定理求出AD即可;
(3)分别求出圆O的面积和三角形ACB的面积,即可得出答案.
(2)根据勾股定理求出AC,根据垂径定理求出AD即可;
(3)分别求出圆O的面积和三角形ACB的面积,即可得出答案.
解答:解:(1)∵AB是直径,
∴∠ACB=90°,
sin∠BAC=
=
;
(2)∵OD⊥AC,OD过O,
∴AD=
AC=6;
(3)阴影部分的面积S=S半圆O-S△ACB
=
×π×(
)2-
×5×12≈36.4,
即图中阴影部分的面积约是36.4.
∴∠ACB=90°,
sin∠BAC=
| BC |
| AB |
| 5 |
| 13 |
(2)∵OD⊥AC,OD过O,
∴AD=
| 1 |
| 2 |
(3)阴影部分的面积S=S半圆O-S△ACB
=
| 1 |
| 2 |
| 13 |
| 2 |
| 1 |
| 2 |
即图中阴影部分的面积约是36.4.
点评:本题考查了圆的面积,三角形的面积,圆周角定理,垂径定理,勾股定理的应用,主要考查学生运用定理进行推理和计算的能力.

练习册系列答案
相关题目
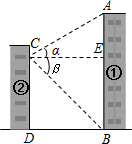 某中学九年级学生在学习“直角三角形的边角关系”时,组织开展测量物体高度的实践活动.在活动中,某小组为了测量校园内①号楼AB的高度(如图),站在②号楼的C处,测得①号楼顶部A处的仰角α=30°,底部B处的俯角β=45°,已知两幢楼的水平距离BD为18米,求①号楼AB的高度.(结果保留根号)
某中学九年级学生在学习“直角三角形的边角关系”时,组织开展测量物体高度的实践活动.在活动中,某小组为了测量校园内①号楼AB的高度(如图),站在②号楼的C处,测得①号楼顶部A处的仰角α=30°,底部B处的俯角β=45°,已知两幢楼的水平距离BD为18米,求①号楼AB的高度.(结果保留根号) 如图,AB是⊙O的直径,AM,BN分别切⊙O于点A,B,CD交AM,BN于点D,C,DO平分∠ADC.
如图,AB是⊙O的直径,AM,BN分别切⊙O于点A,B,CD交AM,BN于点D,C,DO平分∠ADC.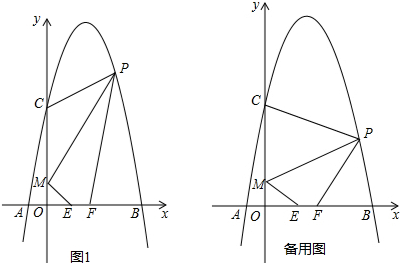
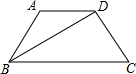 如图,四边形ABCD是等腰梯形,若其四边满足长度的众数为5,平均数为
如图,四边形ABCD是等腰梯形,若其四边满足长度的众数为5,平均数为