题目内容
16.甲、乙二人共同解关于x、y的方程组$\left\{\begin{array}{l}{ax+4y=18①}\\{bx-2y=-1②}\end{array}\right.$时,由于甲看错了方程①中的a,得到方程组的解为$\left\{\begin{array}{l}{x=-3}\\{y=-1}\end{array}\right.$,乙看清了方程②中的b.得到方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$,试计算b2012+(-$\frac{1}{10}$a)2013的值.分析 根据方程组的解的定义,$\left\{\begin{array}{l}{x=-3}\\{y=-1}\end{array}\right.$应满足方程②,$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$应满足方程①,将它们分别代入方程②①,就可得到关于a,b的二元一次方程组,解得a,b的值,即可求得结果.
解答 解:甲看错了①式中x的系数a,解得$\left\{\begin{array}{l}{x=-3}\\{y=-1}\end{array}\right.$,但满足②式的解,所以-3b-2×(-1)=-1,解得b=1,
同理乙看错了②式中y的系数b,解得$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$,满足①式的解,所以a+8=18,解得a=10,
∴b2012+(-$\frac{1}{10}$a)2013=12012+${(-\frac{1}{10}×10)}^{2013}$=0.
点评 此题考查了二元一次方程组的解的定义:一般地,二元一次方程组的两个方程的公共解,叫做二元一次方程组的解.同时考查了二元一次方程组的解的求法.

练习册系列答案
相关题目
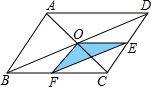 如图,O是平行四边形ABCD对角线的交点,OE∥AD交CD于E,OF∥AB于F,那么S△OEF:S平行四边形ABCD=1:8.
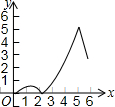
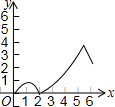
如图,O是平行四边形ABCD对角线的交点,OE∥AD交CD于E,OF∥AB于F,那么S△OEF:S平行四边形ABCD=1:8.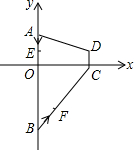 如图,在平面直角坐标系xOy中,四边形ABCD的顶点分别为A(0,2),B(0,-4),C(3,0),D(3,1).点E沿A→B方向运动,点F沿B→C→D方向运动.现E,F两点同时出发,都以每秒1个单位长度的速度运动.设点E的运动时间为x(0≤x≤6)秒,△OEF的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( )
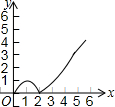
如图,在平面直角坐标系xOy中,四边形ABCD的顶点分别为A(0,2),B(0,-4),C(3,0),D(3,1).点E沿A→B方向运动,点F沿B→C→D方向运动.现E,F两点同时出发,都以每秒1个单位长度的速度运动.设点E的运动时间为x(0≤x≤6)秒,△OEF的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( )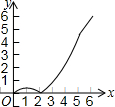
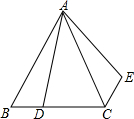 如图,在等边三角形ABC中,AB=6,D是BC上一点,且BC=3BD,△ABD绕点A旋转后得到△ACE,则CE的长度为( )
如图,在等边三角形ABC中,AB=6,D是BC上一点,且BC=3BD,△ABD绕点A旋转后得到△ACE,则CE的长度为( ) 已知:如图,△ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD.
已知:如图,△ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD.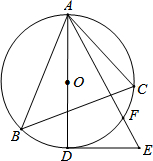 如图,已知△ABC是⊙O的圆内接三角形,AD为⊙O的直径,DE为⊙O的切线,AE交⊙O于点F,∠C=∠E.
如图,已知△ABC是⊙O的圆内接三角形,AD为⊙O的直径,DE为⊙O的切线,AE交⊙O于点F,∠C=∠E.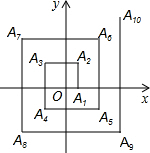 在平面直角坐标系中,点A从原点出发沿x轴正方向移动1个单位到A1,逆时针旋转90°前进2个单位到A2…逆时针旋转90°前进2015个单位到点A2015,则A2015的坐标是(1008,-1006).
在平面直角坐标系中,点A从原点出发沿x轴正方向移动1个单位到A1,逆时针旋转90°前进2个单位到A2…逆时针旋转90°前进2015个单位到点A2015,则A2015的坐标是(1008,-1006).