题目内容

4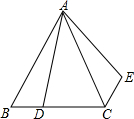．如图，在等边三角形ABC中，AB=6，D是BC上一点，且BC=3BD，△ABD绕点A旋转后得到△ACE，则CE的长度为（　　）
A．6B．5C．3D．2

分析 由在等边三角形ABC中，AB=6，D是BC上一点，且BC=3BD，根据等边三角形的性质，即可求得BD的长，然后由旋转的性质，即可求得CE的长度．

解答 解：∵在等边三角形ABC中，AB=6，
∴BC=AB=6，
∵BC=3BD，
∴BD=$\frac{1}{3}$BC=2，
∵△ABD绕点A旋转后得到△ACE，
∴△ABD≌△ACE，
∴CE=BD=2．
故选：D．

点评 此题考查了旋转的性质与等边三角形的性质．此题难度不大，注意旋转中的对应关系．

练习册系列答案
相关题目
14．抛物线y=（x+4）2+3的顶点坐标是（　　）
A．（4，-3）B．（-4，-3）C．（4，3）D．（-4，3）
15．分式方程$\frac{2}{x-1}$=$\frac{3}{x+2}$的解是（　　）
A．x=1B．x=-1C．x=7D．x=-7
12．某市为鼓励市民节约用水和加强对节水的管理，制定了以下每月每户用水的收费标准：
①用水量不超过8立方米时，每立方米收费0.8元，并加收每立方米0.2元的污水处理费；
②用水量超过8立方米时，在①的基础上，超过8立方米的部分，每立方米收费1.6元，并加收每立方米0.4元的污水处理费．
设某户一个月的用水量为x立方米，应交水费为y元
（1）试分析对①②两种情况，求出y关于x的函数解析式，并写出函数的定义域；
（2）如果该户一个月的水费为20元，求该户这一个月的用水量．
19．“重百”、“沃尔玛”两家超市出售 同样的保温壶和水杯，保温壶和水杯在两家超市的售价分别一样．已知买1个保温壶和1个水杯要花费60元，买2个保温壶和3个水杯要花费130元．
（1）请问：一个保温壶与一个水杯售价各是多少元？（列方程组求解）
（2）为了迎接“五一劳动节”，两家超市都在搞促销活动，“重百”超市规定：这两种商品都打九折；“沃尔玛”超市规定：买一个保温壶赠送一个水杯．若某单位想要买4个保温壶和15个水杯，如果只能在一家超市购买，请问选择哪家超市购买更合算？请说明理由．
9．我们将1×2×3…×n记作n！，如：5！=1×2×3×4×5；100！=1×2×3…×100；若设S=1×1！+2×2！+3×3！+…+2013×2013！，则S除以2014的余数是（　　）
A．0B．1C．2012D．2013
16．甲、乙二人共同解关于x、y的方程组$\left\{\begin{array}{l}{ax+4y=18①}\\{bx-2y=-1②}\end{array}\right.$时，由于甲看错了方程①中的a，得到方程组的解为$\left\{\begin{array}{l}{x=-3}\\{y=-1}\end{array}\right.$，乙看清了方程②中的b．得到方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$，试计算b2012+（-$\frac{1}{10}$a）2013的值．
10．在正方形ABCD中，动点E，F分别从D，C两点同时出发，以相同的速度在直线DC，CB上移动．
（1）如图1，当点E在边DC上自D向C移动，同时点F在边CB上自C向B移动时，连接AE和DF交于点P，请你写出AE与DF的数量关系和位置关系，并说明理由；
（2）如图2，当E，F分别在边CD，BC的延长线上移动时，连接AE，DF，（1）中的结论还成立吗？（请你直接回答“是”或“否”，不需证明）；连接AC，请你直接写出△ACE为等腰三角形时CE：CD的值；
（3）如图3，当E，F分别在直线DC，CB上移动时，连接AE和DF交于点P，由于点E，F的移动，使得点P也随之运动，请你画出点P运动路径的草图．若AD=2，试求出线段CP的最大值．
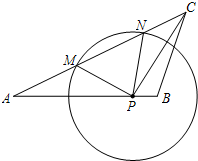11．如图，已知在△ABC中，AB=15，AC=20，tanA=$\frac{1}{2}$，点P在AB边上，⊙P的半径为定长．当点P与点B重合时，⊙P恰好与AC边相切；当点P与点B不重合时，⊙P与AC边相交于点M和点N．
（1）求⊙P的半径；
（2）当AP=$6\sqrt{5}$时，试探究△APM与△PCN是否相似，并说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网