题目内容
7．
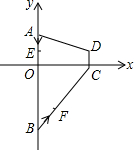如图，在平面直角坐标系xOy中，四边形ABCD的顶点分别为A（0，2），B（0，-4），C（3，0），D（3，1）．点E沿A→B方向运动，点F沿B→C→D方向运动．现E，F两点同时出发，都以每秒1个单位长度的速度运动．设点E的运动时间为x（0≤x≤6）秒，△OEF的面积为y，则下列图象中，能表示y与x的函数关系的图象大致是（ ）| A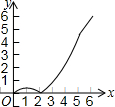． |  | B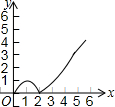． |  | C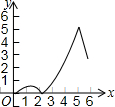． |  | D． |  |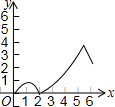
分析 根据动点运动的函数关系式进行判断其图象即可．
解答 解：∵A（0，2），B（0，-4），C（3，0），D（3，1），
∴AB=6，BC=5，CD=1，AD=$\sqrt{10}$，
∵点E沿A→B方向运动，点F沿B→C→D方向运动，且都以每秒1个单位长度的速度运动，
∴设点E的运动时间为x（0≤x≤6）秒，△OEF的面积为y，
可得：当0≤x≤2时，y=$\frac{1}{2}（2-x）•\frac{3}{5}x=\frac{3}{10}x（2-x）$；
当2＜x≤5时，y=$\frac{1}{2}（x-2）\frac{3}{5}x=\frac{3}{10}x（x-2）$；
当5＜x≤6，y=$\frac{1}{2}（x-2）×3=\frac{3}{2}（x-2）$；
由此可得，当0≤x≤2时，图象是抛物线，当2＜x≤5时，图象是抛物线的增函数部分，当5＜x≤6时，图象是一次函数，
故选A．
点评 此题考查函数动点问题，关键是根据题意得出解析式，然后根据解析式判断函数图象．
练习册系列答案
相关题目
17．下列二次根式中，是最简二次根式的是（ ）
| A． | $\sqrt{45}$ | B． | $\sqrt{\frac{1}{3}}$ | C． | $\sqrt{5{a}^{2}}$ | D． | $\sqrt{7}$ |
如图，在△ABC中，点O是边上一个动点，过点O作直线MN∥BC，设MN交∠BCA的平分线于点E，交△BCA的外角平分线于点F．
15．分式方程$\frac{2}{x-1}$=$\frac{3}{x+2}$的解是（ ）
| A． | x=1 | B． | x=-1 | C． | x=7 | D． | x=-7 |