题目内容
9.已知α是锐角,且sin(α-15°)=$\frac{1}{2}$计算:$\sqrt{8}$-4cosα-(π-3.14)0+tanα+($\frac{1}{3}$)-1的值.
分析 首先利用特殊角的三角函数值得出α的度数,再利用负整数指数幂的性质以及零指数幂的性质和特殊角的三角函数值分别化简得出答案.
解答 解:∵sin(α-15°)=$\frac{1}{2}$,
∴α-15°=30°,
则α=45°,
$\sqrt{8}$-4cosα-(π-3.14)0+tanα+($\frac{1}{3}$)-1
=2$\sqrt{2}$-4×$\frac{\sqrt{2}}{2}$-1+1+3
=3.
点评 此题主要考查了负整数指数幂的性质以及零指数幂的性质和特殊角的三角函数值等知识,正确化简各数是解题关键.

练习册系列答案
相关题目
19.如图是一个几何体的三视图,则这个几何体的表面积是( )


| A. | (6+π)cm2 | B. | (12+4π)cm2 | C. | 3πcm2 | D. | 4πcm2 |
20.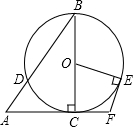 如图,在Rt△ABC中,∠ACB=90°,∠A=56°.以BC为直径的⊙O交AB于点D.E是⊙O上一点,且$\widehat{C{E}}$=$\widehat{CD}$,连接OE.过点E作EF⊥OE,交AC的延长线于点F,则∠F的度数为( )
如图,在Rt△ABC中,∠ACB=90°,∠A=56°.以BC为直径的⊙O交AB于点D.E是⊙O上一点,且$\widehat{C{E}}$=$\widehat{CD}$,连接OE.过点E作EF⊥OE,交AC的延长线于点F,则∠F的度数为( )
 如图,在Rt△ABC中,∠ACB=90°,∠A=56°.以BC为直径的⊙O交AB于点D.E是⊙O上一点,且$\widehat{C{E}}$=$\widehat{CD}$,连接OE.过点E作EF⊥OE,交AC的延长线于点F,则∠F的度数为( )
如图,在Rt△ABC中,∠ACB=90°,∠A=56°.以BC为直径的⊙O交AB于点D.E是⊙O上一点,且$\widehat{C{E}}$=$\widehat{CD}$,连接OE.过点E作EF⊥OE,交AC的延长线于点F,则∠F的度数为( )| A. | 92° | B. | 108° | C. | 112° | D. | 124° |
4.如表是一个4×4(4行4列共16个“数”组成)的奇妙方阵,从这个方阵中选四个“数”,而且这四个“数”中的任何两个不在同一行,也不在同一列,有很多选法,把每次选出的四个“数”相加,其和是定值,则方阵中第三行三列的“数”是( )
| 30 | $\sqrt{4}$ | 2$\sqrt{3}$sin60° | 22 |
| -3 | -2 | -$\sqrt{2}$sin45° | 0 |
| |-5| | 6 | 23 | |
| ($\frac{1}{3}$)-1 | 4 | $\sqrt{25}$ | ($\frac{1}{6}$)-1 |
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
1.下列运算正确的是( )
| A. | a2•a3=a6 | B. | a8÷a2=a4 | C. | (a3)2=a5 | D. | (ab)2=a2b2 |
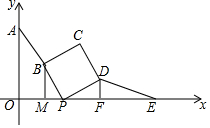 如图,已知A(0,4),E(8,0),点P(a,0)是线段OE上的动点,点B为AP的中点,以BP为边向右边作正方形PBCD,过点B作BM⊥x轴于点M,过点D作DF⊥x轴于点F,连接DE.
如图,已知A(0,4),E(8,0),点P(a,0)是线段OE上的动点,点B为AP的中点,以BP为边向右边作正方形PBCD,过点B作BM⊥x轴于点M,过点D作DF⊥x轴于点F,连接DE. 2016年11月1日,万众期待的歼20战机现身珠海航展,上午9时,某航空爱好者在地面C处测得点A处的歼20战机的仰角是30°,正以300米/秒的速度向正西方向航行,1分钟后到达点B处,此时航空爱好者测得其仰角为45°,如图所示,求歼20战机在珠海航展表演时的飞行高度.(精确到100米)参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73.
2016年11月1日,万众期待的歼20战机现身珠海航展,上午9时,某航空爱好者在地面C处测得点A处的歼20战机的仰角是30°,正以300米/秒的速度向正西方向航行,1分钟后到达点B处,此时航空爱好者测得其仰角为45°,如图所示,求歼20战机在珠海航展表演时的飞行高度.(精确到100米)参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73.