题目内容
20.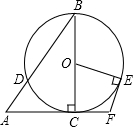 如图,在Rt△ABC中,∠ACB=90°,∠A=56°.以BC为直径的⊙O交AB于点D.E是⊙O上一点,且$\widehat{C{E}}$=$\widehat{CD}$,连接OE.过点E作EF⊥OE,交AC的延长线于点F,则∠F的度数为( )
如图,在Rt△ABC中,∠ACB=90°,∠A=56°.以BC为直径的⊙O交AB于点D.E是⊙O上一点,且$\widehat{C{E}}$=$\widehat{CD}$,连接OE.过点E作EF⊥OE,交AC的延长线于点F,则∠F的度数为( )| A. | 92° | B. | 108° | C. | 112° | D. | 124° |
分析 直接利用互余的性质再结合圆周角定理得出∠COE的度数,再利用四边形内角和定理得出答案.
解答 解:∵∠ACB=90°,∠A=56°,
∴∠ABC=34°,
∵$\widehat{C{E}}$=$\widehat{CD}$,
∴2∠ABC=∠COE=68°,
又∵∠OCF=∠OEF=90°,
∴∠F=360°-90°-90°-68°=112°.
故选:C.
点评 此题主要考查了圆周角定理以及四边形内角和定理,正确得出∠OCE的度数是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.有四个数-6,-4,-3,-1,其中比-2大的数是( )
| A. | -6 | B. | -4 | C. | -3 | D. | -1 |
8.下列运算结果为a5的是( )
| A. | a2+a3 | B. | a•a5 | C. | (a3)2 | D. | a6÷a |
15.已知下列命题:①若|x|=3,则x=3;②当a>b时,若c>0,则ac>bc;③直角三角形中斜边上的中线等于斜边的一半;④内错角相等.
其中原命题与逆命题均为真命题的个数是( )
其中原命题与逆命题均为真命题的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,网格纸上正方形小格的边长为1.图中线段AB和点P绕着同一个点做相同的旋转,分别得到线段A'B'和点P',则点P'所在的单位正方形区域是( )
如图,网格纸上正方形小格的边长为1.图中线段AB和点P绕着同一个点做相同的旋转,分别得到线段A'B'和点P',则点P'所在的单位正方形区域是( )